Мотивация
В области морской инженерии и управления прогнозированием и состоянием (PHM) отрасль сталкивается с двумя давними проблемами:
- Дефицит данных: Судовые дизельные двигатели (особенно главные двигатели океанских судов) являются сердцем судна. Серьезная поломка в море может привести к потере хода, посадке на мель или даже катастрофе. Поэтому при проектировании в них закладываются чрезвычайно высокие коэффициенты запаса прочности, и вероятность серьезных отказов сама по себе очень низка. Кроме того, в судоходной отрасли действуют строгие системы профилактического обслуживания (например, плановый ремонт по часам наработки). Подавляющее большинство изнашиваемых деталей принудительно заменяются до того, как они действительно выйдут из строя и сгенерируют данные об отказе. Это приводит к наличию большого объема данных о нормальной работе и раннем износе, но к крайней нехватке реальных данных о полных отказах или серьезных неисправностях.
- Проблема «Черного ящика»: Поскольку модели глубокого обучения обычно непрозрачны, инженерам трудно доверять им, если невозможно объяснить физические причины неисправности. В судоходной отрасли, строго регулируемой классификационными обществами, эта непрозрачность критична. Если ИИ ошибочно диагностирует (или пропустит) задир поршня или поломку коленчатого вала, и система не сможет отследить, является ли ошибка следствием смещения данных, дефекта алгоритма или дрейфа датчика, такая невозможность отслеживания неприемлема при расследовании морских аварий.
Для решения этих задач мы предложили метод TSRF. Объединяя физические механистические модели с передовыми методами объяснимости и используя высокоточные имитационные модели для решения проблемы нехватки данных, мы гарантируем, что диагностические решения соответствуют фундаментальным принципам термодинамики.
Методология
Рабочий процесс данного исследования включает следующие четыре основных этапа (см. рисунок):
- Термодинамическое моделирование: Вместо того чтобы полагаться исключительно на физические испытательные стенды, мы построили высокоточную одномерную термодинамическую модель шестицилиндрового судового дизельного двигателя. Модель была строго откалибрована на основе реальных эксплуатационных данных, с погрешностью моделирования менее 5%.
- Внедрение неисправностей: На основе откалиброванной модели мы смоделировали пять специфических неисправностей камеры сгорания (таких как трещины в головке цилиндра, прогар поршня и т.д.) путем точной настройки физических параметров, создав набор данных, охватывающий различные степени реальных неисправностей двигателя.
- Отбор признаков на основе SHAP: Мы использовали значения SHAP для количественной идентификации ключевых признаков, отобрав 14 критических параметров, определяющих диагностическое решение.
- Классификационная диагностика: Используя этот физически обогащенный набор данных, мы обучили классификатор «Случайный лес» (RF) и добились высокоточной диагностики неисправностей.
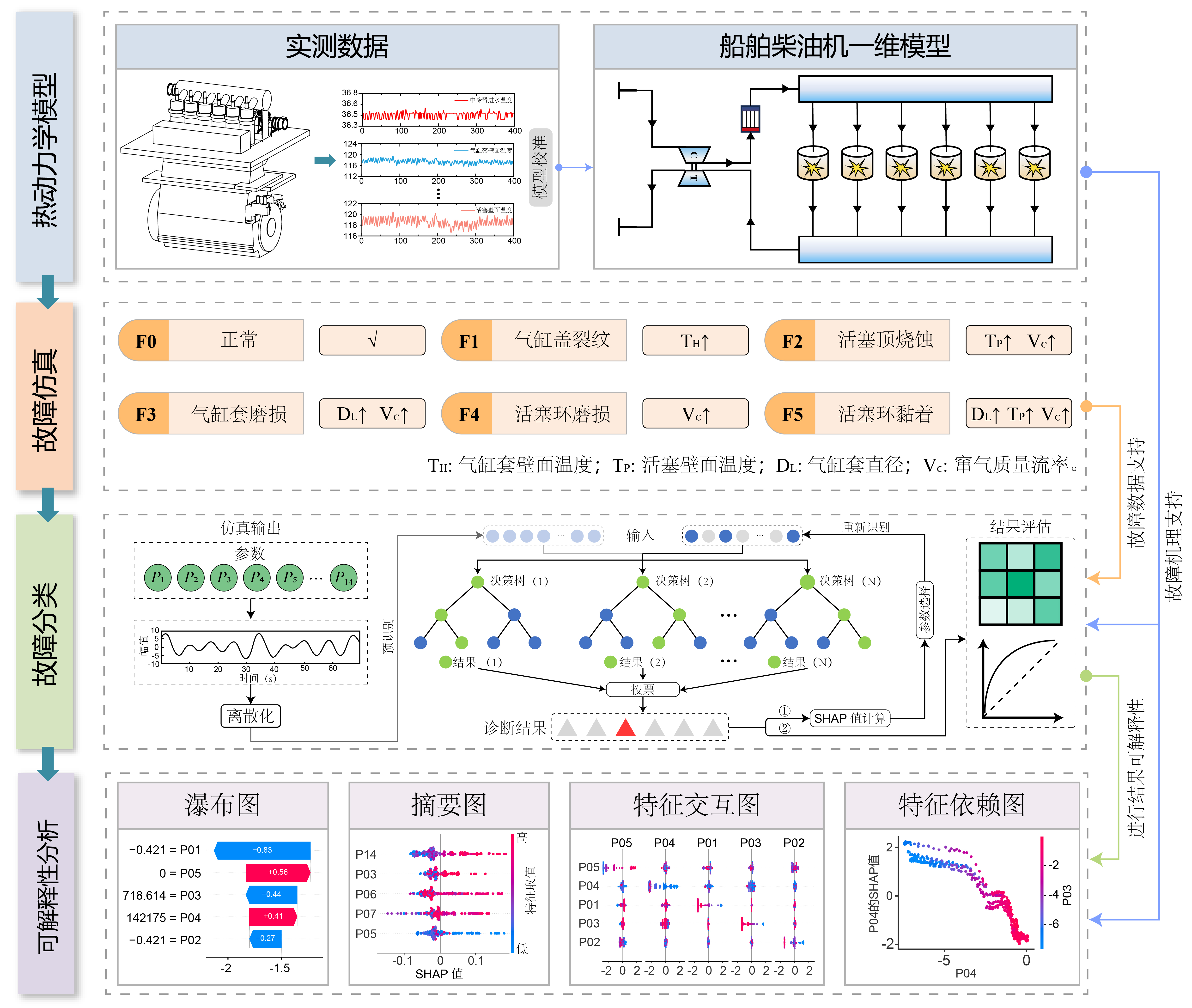
Рис. 1: Архитектура метода TSRF.
Детали термодинамического моделирования
Для обеспечения высокой точности мы построили одномерную имитационную модель дизельного двигателя. Эта механистическая модель обеспечивает баланс между физической точностью и вычислительной эффективностью, необходимой для генерации наборов данных.
Топология модели
Система двигателя дискретизирована как сеть жидкостных трубопроводов и функциональных компонентов:
- Основной силовой агрегат: Шестицилиндровая, двухтактная рядная конфигурация.
- Газовоздушная система: Впускной/выпускной коллекторы (PL1, PL2) соединены сложной сетью трубопроводов.
- Система наддува: Турбокомпрессор (TC1), соединенный с интеркулером (CO1).
Калибровка и валидация
Перед внедрением неисправностей базовая модель была строго откалибрована на основе измеренных данных.
- Источник данных: Реальные эксплуатационные данные судна, полученные через модуль сбора данных (DCM).
- Валидация: Отклонения ключевых параметров (таких как мощность, температура выхлопных газов) строго контролировались в пределах погрешности ±5% .
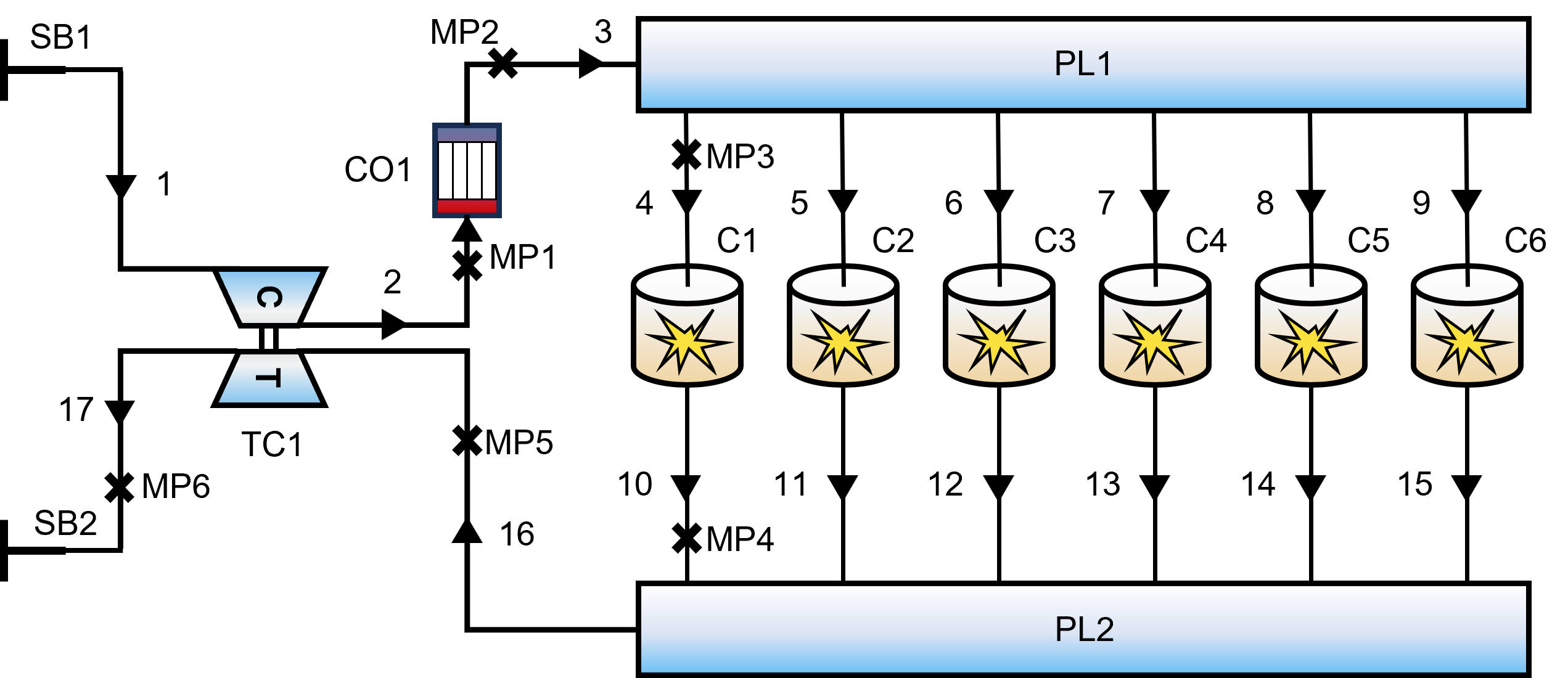
Рис. 2: Схема одномерной термодинамической модели дизельного двигателя.
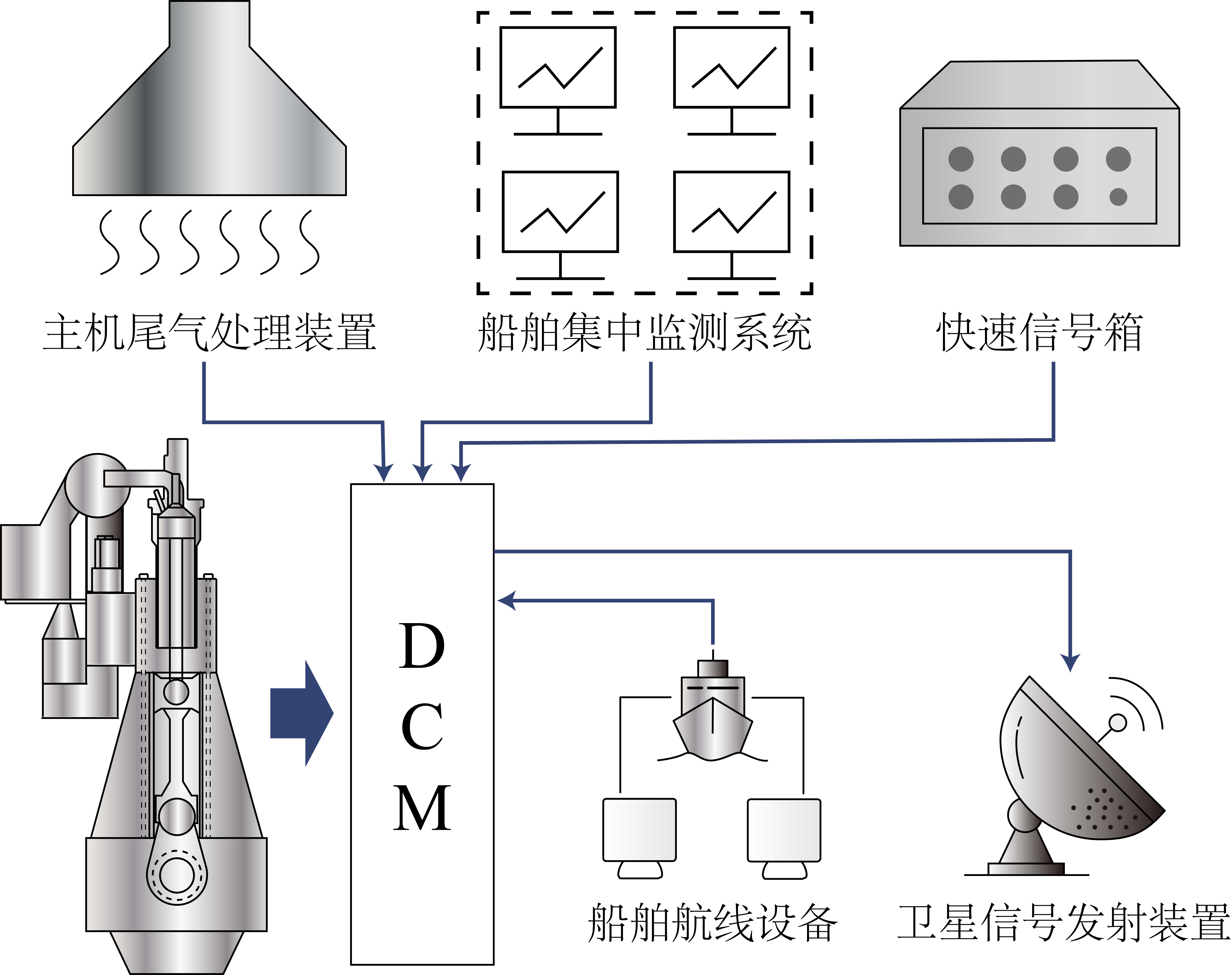
Рис. 5: Модуль сбора данных (DCM).
Механизм внедрения неисправностей
Поскольку одномерные модели не могут напрямую отображать трехмерные структурные дефекты, мы применили метод феноменологического отображения для перевода механизмов физической деградации в эквивалентные смещения термодинамических параметров.
| Тип неисправности | Физический механизм | Реализация моделирования |
|---|---|---|
| F1: Трещина ГБЦ | Нарушение теплопроводности. | Повышение температуры поверхности головки блока цилиндров ($T_H$) до 346°C. |
| F2: Прогар поршня | Потеря материала и нарушение герметичности. | Повышение температуры поршня ($T_P$) + незначительный прорыв газов (0.01 кг/с). |
| F3: Износ втулки | Увеличение диаметра цилиндра из-за износа. | Увеличение диаметра + сильный прорыв газов (0.03 кг/с). |
| F4: Износ колец | Утечка газа. | Регулировка массового расхода прорыва газов (0.02 кг/с). |
| F5: Залегание колец | Увеличение трения и нарушение герметичности. | Изменение диаметра цилиндра + повышение температуры втулки + прорыв газов. |
Анализ интерпретируемости
Ключевая инновация данного исследования заключается в смещении фокуса с вопроса «Какая это неисправность?» на «Почему диагностирована эта неисправность?». Мы продемонстрировали эту возможность на примере анализа износа поршневых колец (F4):
- Локальное объяснение (Каскадная диаграмма): Каскадная диаграмма раскрывает конкретную логику прогнозирования. Например, модель предсказала «износ поршневых колец», потому что тепловой поток прорыва газов (P06) и массовый расход прорыва газов (P07) имели определенные значения, что повысило вероятность прогнозирования этой неисправности. Это согласуется с физическими законами: износ колец нарушает герметичность, приводя к утечке газа (прорыву газов).
- Глобальное объяснение (Диаграмма роя пчел): Глобальный анализ выявляет общие закономерности, усвоенные моделью. Мы обнаружили, что низкое значение давления выхлопных газов перед турбиной (P11) является сильным индикатором износа поршневых колец. С физической точки зрения это логично: изношенные кольца приводят к утечке газа из цилиндра, тем самым уменьшая энергию, доступную для привода турбины.
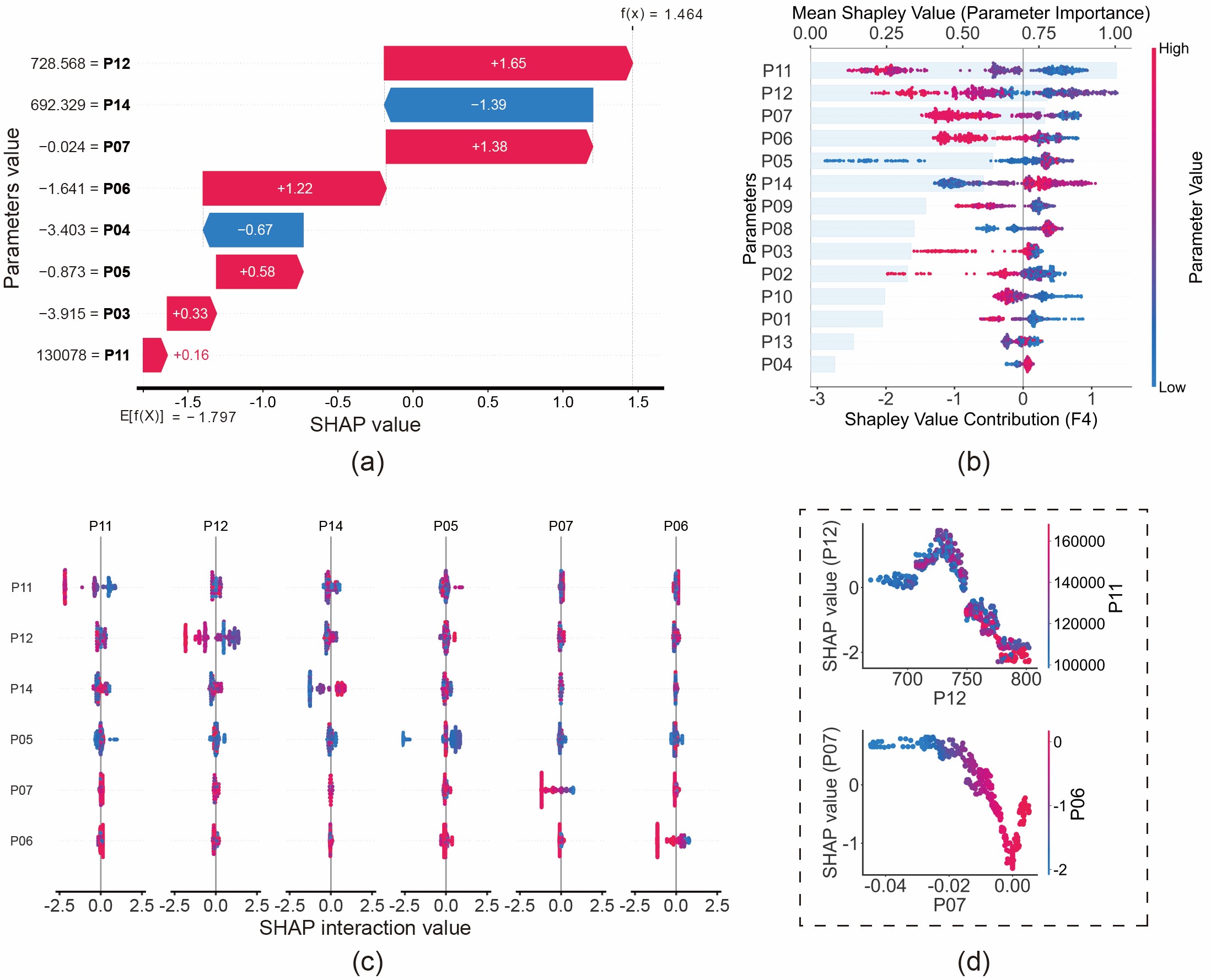
Рис. 11: Анализ неисправности износа поршневых колец (F4) на основе значений SHAP: (a) Каскадная диаграмма; (b) Диаграмма роя пчел; (c) Диаграмма взаимодействия; (d) Диаграмма зависимости.
Посмотреть код визуализации SHAP (Python)
Если вас интересуют детали реализации приведенных выше графиков, вот пример кода для создания каскадной диаграммы, диаграммы роя пчел, диаграммы взаимодействия и диаграммы зависимости.👇
Основные моменты исследования
Мы считаем, что данная работа внесла следующий ключевой вклад в эту область:
- Созданы параметризованные модели для пяти типичных неисправностей компонентов камеры сгорания судовых дизельных двигателей.
- Подтверждена эффективность метода SHAP путем сравнения с несколькими методами отбора признаков.
- Предложен новый взгляд на объяснимую диагностику неисправностей путем объединения методов, основанных на данных, с термодинамическими механистическими моделями.