Motywacja badawcza
W dziedzinie inżynierii morskiej oraz Prognostyki i Zarządzania Stanem Zdrowia (PHM), przemysł stoi przed dwoma długoterminowymi wąskimi gardłami:
- Niedobór danych: Okrętowe silniki Diesla (szczególnie silniki główne statków oceanicznych) są sercem statku. Poważna awaria na morzu może prowadzić do utraty napędu, wejścia na mieliznę lub nawet katastrofy morskiej. Dlatego ich współczynniki bezpieczeństwa w projektowaniu są niezwykle wysokie, a prawdopodobieństwo poważnych awarii jest z natury bardzo niskie. Ponadto przemysł żeglugowy wdraża rygorystyczne systemy konserwacji zapobiegawczej (takie jak planowe remonty oparte na godzinach pracy). Zdecydowana większość części zużywających się jest przymusowo wymieniana, zanim faktycznie ulegną awarii i wygenerują dane o uszkodzeniu. Prowadzi to do obfitości danych o stanie prawidłowym i wczesnym zużyciu, ale do skrajnego braku rzeczywistych danych o całkowitej awarii lub poważnych usterkach.
- Problem "Czarnej Skrzynki": Ponieważ modele głębokiego uczenia zazwyczaj nie są transparentne, inżynierom trudno jest im zaufać, jeśli nie potrafią wyjaśnić fizycznych przyczyn awarii. W przemyśle żeglugowym, ściśle regulowanym przez towarzystwa klasyfikacyjne, ten brak przejrzystości jest krytyczny. Jeśli AI błędnie zdiagnozuje (lub pominie) zatarcie tłoka lub pęknięcie wału korbowego, a system nie może prześledzić, czy błąd wynika z obciążenia danych, wady algorytmu czy dryfu czujnika, ta brak identyfikowalności jest nie do przyjęcia w dochodzeniach w sprawach wypadków morskich.
Aby sprostać tym wyzwaniom, zaproponowaliśmy metodę TSRF. Łącząc oparte na fizyce modele mechanistyczne z zaawansowanymi technikami wyjaśnialności i wykorzystując modele symulacyjne o wysokiej wierności do rozwiązania problemu niedoboru danych, zapewniamy, że decyzje diagnostyczne są zgodne z podstawowymi zasadami termodynamiki.
Metodologia
Przepływ pracy w tym badaniu obejmuje następujące cztery główne etapy (jak pokazano na rysunku):
- Modelowanie termodynamiczne: Zamiast polegać wyłącznie na fizycznych stanowiskach badawczych, zbudowaliśmy jednowymiarowy model termodynamiczny o wysokiej wierności sześciocylindrowego okrętowego silnika Diesla. Model został rygorystycznie skalibrowany na podstawie rzeczywistych danych operacyjnych, utrzymując błąd symulacji poniżej 5%.
- Wstrzykiwanie uszkodzeń: Na podstawie skalibrowanego modelu zasymulowaliśmy pięć specyficznych uszkodzeń komory spalania (takich jak pęknięcia głowicy cylindra, ablacja tłoka itp.), precyzyjnie dostrajając parametry fizyczne, generując w ten sposób zbiór danych obejmujący różne stopnie rzeczywistych uszkodzeń silnika.
- Selekcja cech oparta na SHAP: Wykorzystaliśmy wartości SHAP do ilościowej identyfikacji kluczowych cech, wybierając 14 krytycznych parametrów dominujących w decyzji diagnostycznej.
- Diagnostyka klasyfikacyjna: Korzystając z tego fizycznie wzbogaconego zbioru danych, wytrenowaliśmy klasyfikator Lasu Losowego (RF) i osiągnęliśmy wysoką precyzję diagnostyki uszkodzeń.
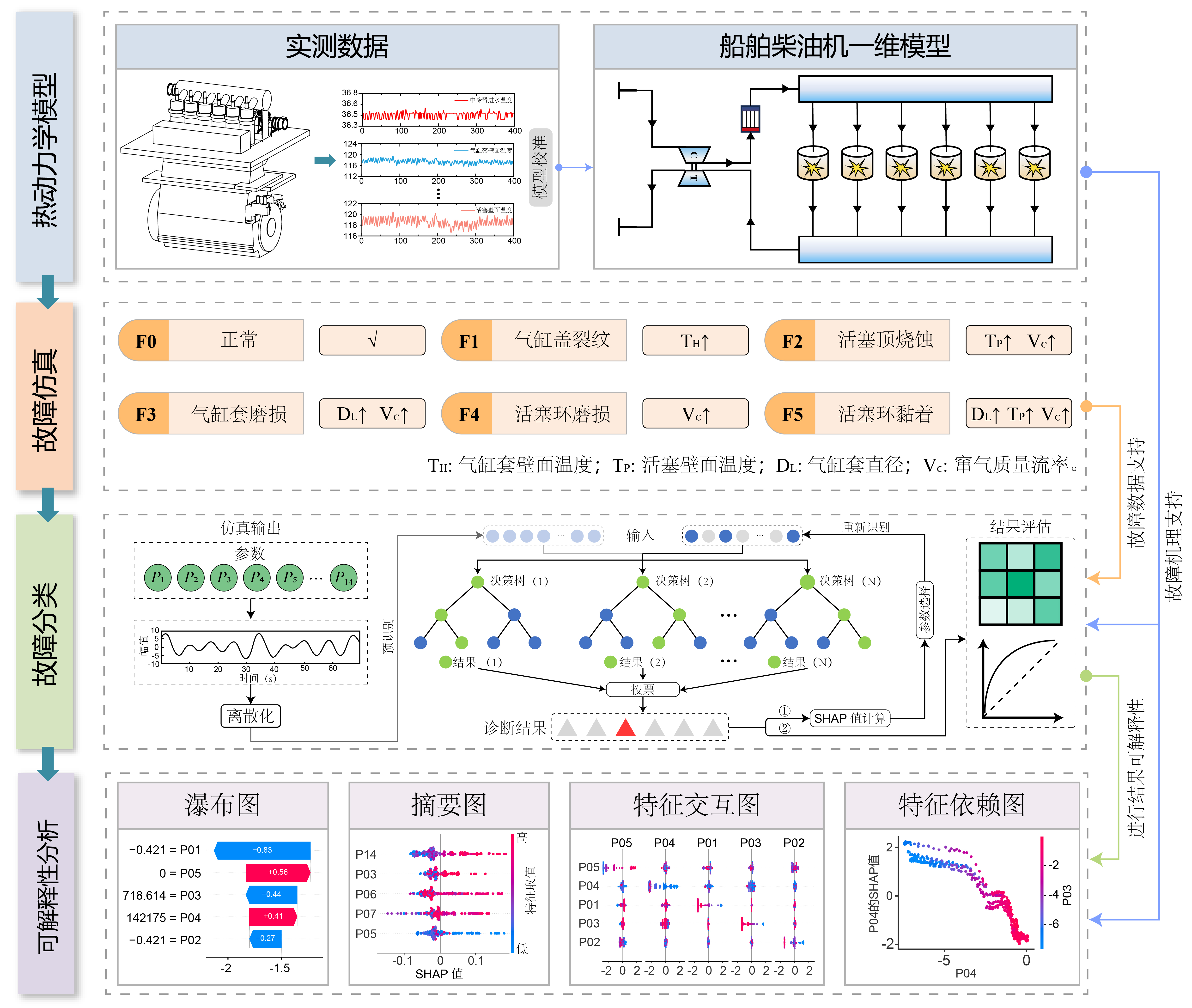
Rys. 1: Architektura metody TSRF.
Szczegóły modelowania termodynamicznego
Aby zapewnić wysoką wierność, zbudowaliśmy jednowymiarowy model symulacyjny silnika Diesla. Ten model mechanistyczny zachowuje równowagę między dokładnością fizyczną a wydajnością obliczeniową wymaganą do generowania zbioru danych.
Topologia modelu
System silnika jest zdyskretyzowany jako sieć rurociągów płynów i komponentów funkcjonalnych:
- Główna jednostka napędowa: Konfiguracja rzędowa, sześć cylindrów, dwusuw.
- Układ powietrzny: Kolektory dolotowe/wylotowe (PL1, PL2) są połączone złożoną siecią rur.
- Układ doładowania: Turbosprężarka (TC1) sprzężona z chłodnicą międzystopniową (CO1).
Kalibracja i walidacja
Przed przystąpieniem do wstrzykiwania uszkodzeń, model bazowy został rygorystycznie skalibrowany na podstawie danych pomiarowych.
- Źródło danych: Rzeczywiste dane operacyjne statku uzyskane za pośrednictwem Modułu Akwizycji Danych (DCM).
- Walidacja: Odchylenia kluczowych parametrów (takich jak moc, temperatura spalin) były ściśle kontrolowane w zakresie błędu ±5% .
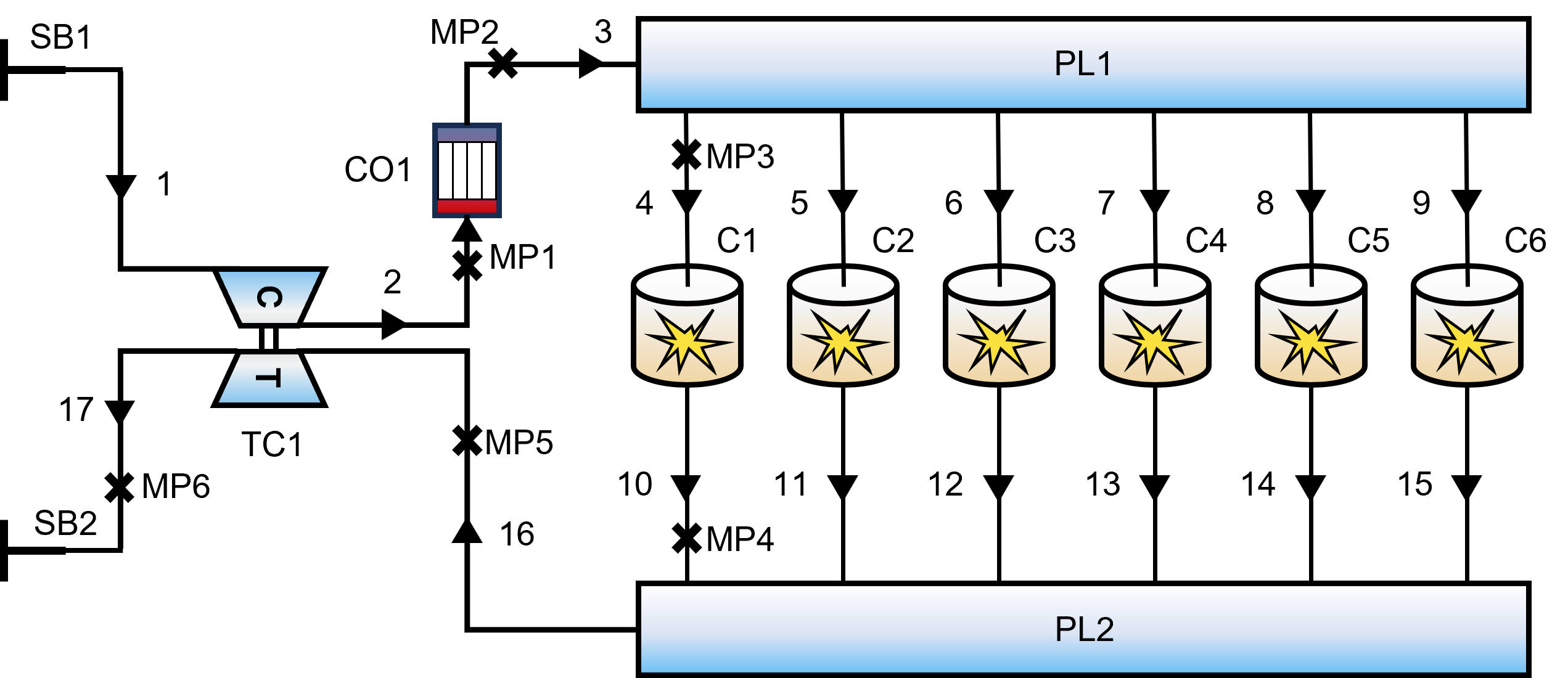
Rys. 2: Schemat jednowymiarowego modelu termodynamicznego silnika Diesla.
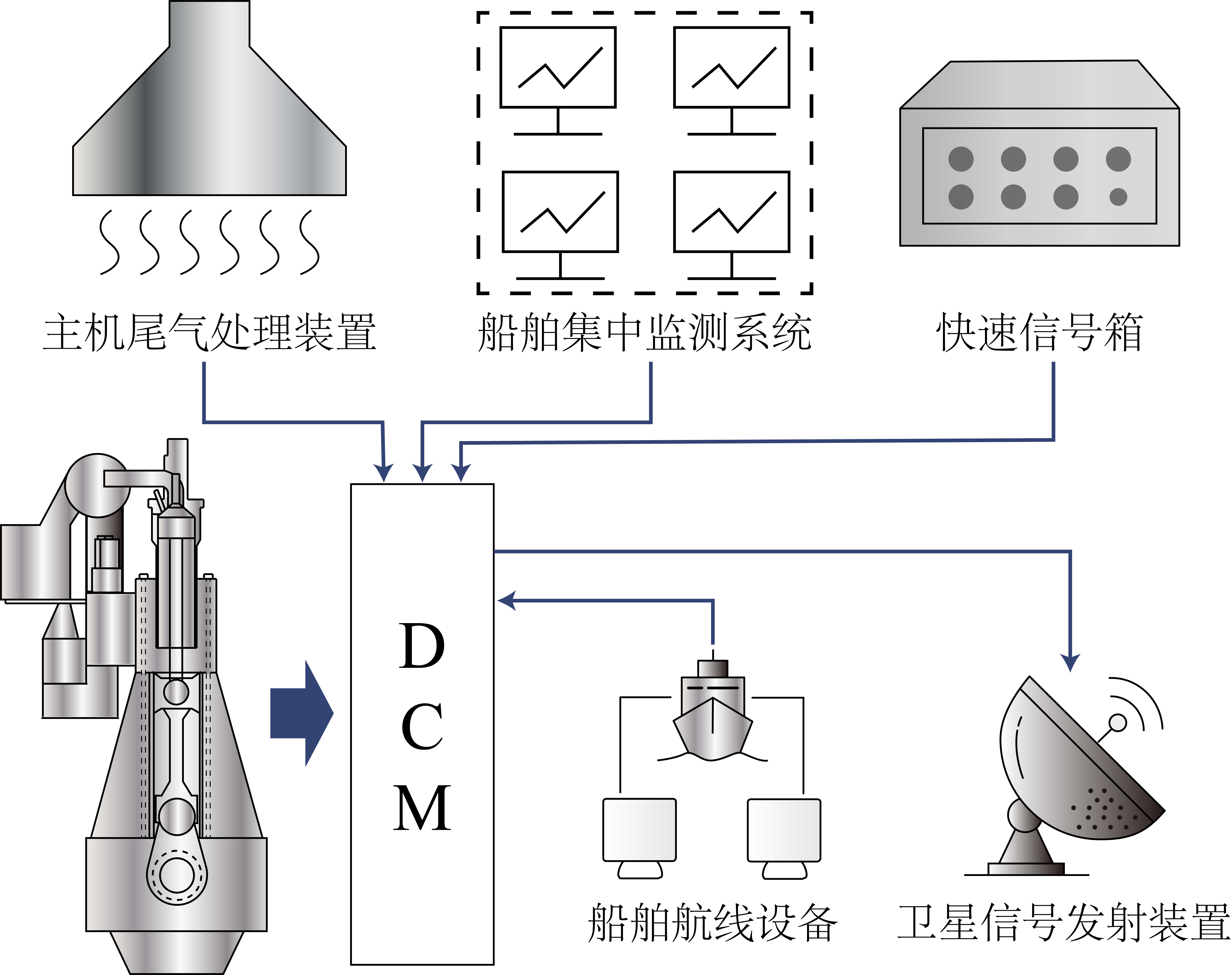
Rys. 5: Moduł Akwizycji Danych (DCM).
Mechanizm wstrzykiwania uszkodzeń
Ponieważ modele jednowymiarowe nie mogą bezpośrednio reprezentować trójwymiarowych wad strukturalnych, przyjęliśmy metodę mapowania fenomenologicznego w celu przetłumaczenia mechanizmów degradacji fizycznej na równoważne przesunięcia parametrów termodynamicznych.
| Typ uszkodzenia | Mechanizm fizyczny | Implementacja modelowania |
|---|---|---|
| F1: Pęknięcie głowicy cylindra | Utrudnione przewodzenie ciepła. | Podniesienie temperatury powierzchni głowicy cylindra ($T_H$) do 346°C. |
| F2: Ablacja tłoka | Utrata materiału i awaria uszczelnienia. | Podniesienie temperatury tłoka ($T_P$) + niewielkie przedmuchy (blow-by) (0,01 kg/s). |
| F3: Zużycie tulei | Powiększenie średnicy cylindra z powodu zużycia. | Zwiększenie średnicy + silne przedmuchy (0,03 kg/s). |
| F4: Zużycie pierścieni | Wyciek gazu. | Regulacja masowego natężenia przepływu przedmuchów (0,02 kg/s). |
| F5: Zapieczenie pierścieni | Zwiększone tarcie i awaria uszczelnienia. | Zmiana średnicy cylindra + wzrost temperatury tulei + przedmuchy. |
Analiza wyjaśnialności
Główna innowacja tego badania polega na przesunięciu uwagi z "Co to za usterka?" na "Dlaczego zdiagnozowano tę usterkę?". Zademonstrowaliśmy tę zdolność poprzez analizę zużycia pierścieni tłokowych (F4):
- Wyjaśnienie lokalne (Wykres kaskadowy): Wykres kaskadowy rozkłada na czynniki pierwsze konkretną logikę predykcji. Na przykład model przewidział "zużycie pierścieni", ponieważ strumień ciepła przedmuchów (P06) i masowe natężenie przepływu przedmuchów (P07) wykazały określone wartości, zwiększając w ten sposób prawdopodobieństwo predykcji tej usterki. Jest to zgodne z prawami fizyki: zużycie pierścieni niszczy uszczelnienie, prowadząc do wycieku gazu (przedmuchów).
- Wyjaśnienie globalne (Wykres roju): Analiza globalna ujawnia ogólne prawa, których nauczył się model. Odkryliśmy, że niska wartość ciśnienia spalin przed turbiną (P11) jest silnym wskaźnikiem zużycia pierścieni. Z fizycznego punktu widzenia jest to spójne: zużyte pierścienie powodują wyciek gazu z cylindra, zmniejszając w ten sposób energię dostępną do napędzania turbiny.
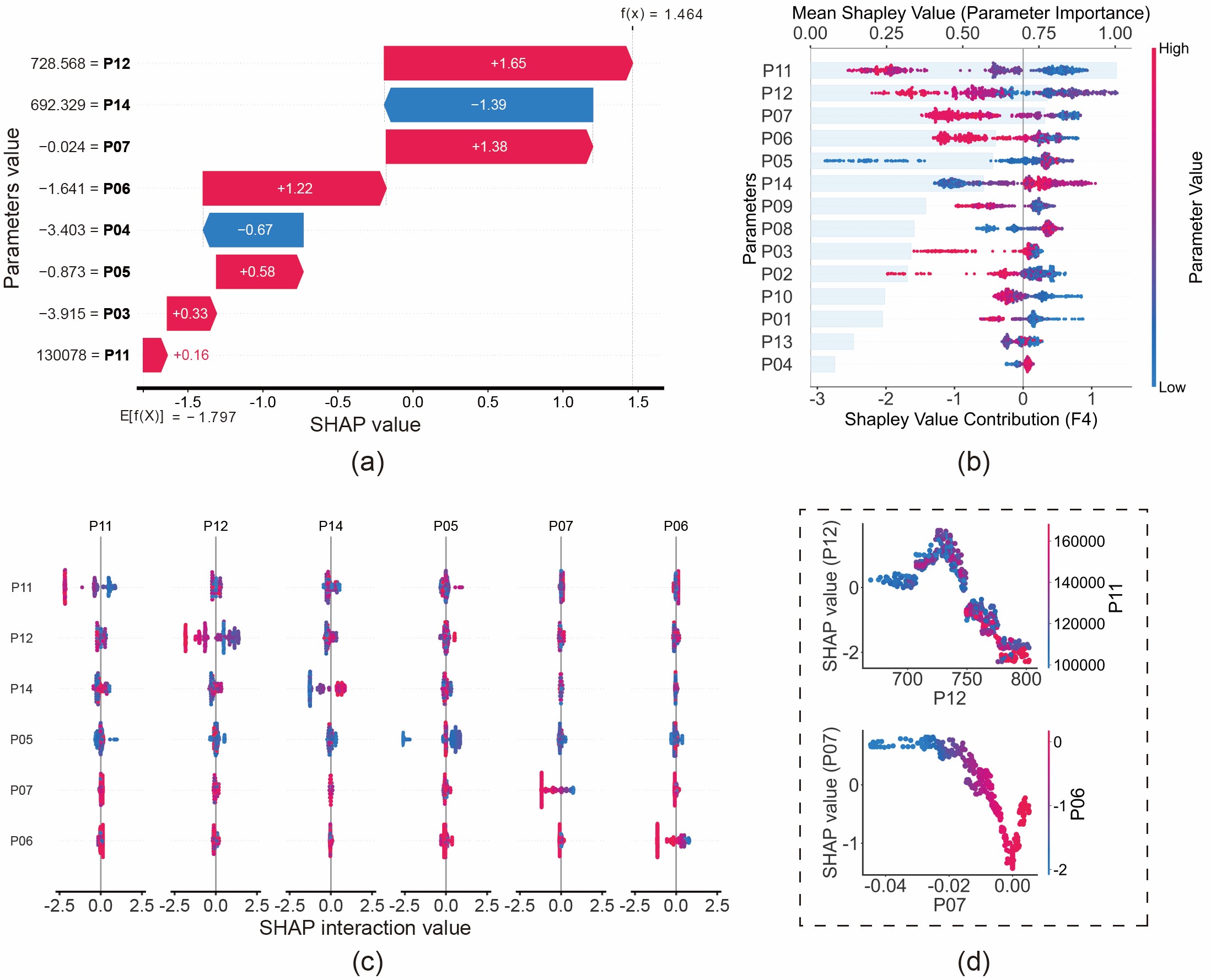
Rys. 11: Analiza usterki zużycia pierścieni tłokowych (F4) na podstawie wartości SHAP: (a) Wykres kaskadowy; (b) Wykres roju; (c) Wykres interakcji; (d) Wykres zależności.
Zobacz kod wizualizacji SHAP (Python)
Jeśli interesują Cię szczegóły implementacji powyższych wykresów, oto przykładowy kod do generowania wykresów kaskadowych, roju, interakcji i zależności.👇
Najważniejsze punkty badań
Uważamy, że ta praca wniosła następujący kluczowy wkład w tę dziedzinę:
- Ustanowienie sparametryzowanych modeli dla pięciu typowych uszkodzeń elementów komory spalania okrętowych silników Diesla.
- Walidacja skuteczności metody SHAP poprzez porównanie z wieloma metodami selekcji cech.
- Zapewnienie nowej perspektywy dla wyjaśnialnej diagnostyki uszkodzeń poprzez połączenie metod opartych na danych z termodynamicznymi modelami mechanicznymi.