Onderzoeksmotivatie
Op het gebied van maritieme techniek en Prognostics & Health Management (PHM) wordt de industrie geconfronteerd met twee langdurige knelpunten:
- Dataschaarste: Scheepsdieselmotoren (met name de hoofdmotoren van zeeschepen) zijn het hart van het schip. Een ernstige storing op zee kan leiden tot verlies van voortstuwing, stranding of zelfs maritieme rampen. Daarom zijn hun veiligheidsfactoren bij het ontwerp extreem hoog en is de kans op ernstige storingen inherent erg laag. Bovendien hanteert de scheepvaartindustrie strikte preventieve onderhoudssystemen (zoals geplande revisies op basis van bedrijfsuren). De overgrote meerderheid van slijtageonderdelen wordt gedwongen vervangen voordat ze daadwerkelijk falen en foutdata genereren. Dit leidt tot een overvloed aan gezondheidsdata en data over vroege slijtage, maar een extreem gebrek aan echte data over volledig falen of ernstige defecten.
- Het "Black Box"-probleem: Aangezien deep learning-modellen doorgaans een gebrek aan transparantie hebben, is het voor ingenieurs moeilijk om ze te vertrouwen als ze de fysieke oorzaken van een fout niet kunnen verklaren. In de scheepvaartindustrie, die strikt gereguleerd wordt door classificatiebureaus, is deze ondoorzichtigheid kritiek. Als AI ten onrechte een zuigervreter (piston scuffing) of krukasbreuk diagnosticeert (of mist), en het systeem niet kan achterhalen of de fout voortkomt uit databias, een algoritmedefect of sensordrift, is deze onherleidbaarheid onacceptabel bij onderzoeken naar maritieme ongevallen.
Om deze uitdagingen aan te gaan, hebben we de TSRF-methode voorgesteld. Door fysica-gebaseerde mechanistische modellen te combineren met geavanceerde verklaringstechnieken en gebruik te maken van high-fidelity simulatiemodellen om het probleem van dataschaarste op te lossen, garanderen we dat diagnosebeslissingen in overeenstemming zijn met fundamentele thermodynamische principes.
Methodologie
De workflow van deze studie omvat de volgende vier hoofdfasen (zoals weergegeven in de afbeelding):
- Thermodynamische modellering: In plaats van uitsluitend te vertrouwen op fysieke testbanken, hebben we een high-fidelity eendimensionaal thermodynamisch model van een zescilinder scheepsdieselmotor gebouwd. Het model werd rigoureus gekalibreerd op basis van echte operationele data, waarbij de simulatiefout onder de 5% werd gehouden.
- Foutinjectie: Op basis van het gekalibreerde model simuleerden we vijf specifieke fouten in de verbrandingskamer (zoals cilinderkopscheuren, zuigerablatie, enz.) door fysieke parameters fijn te regelen, waardoor een dataset werd gegenereerd die verschillende gradaties van echte motorfouten dekt.
- Op SHAP gebaseerde feature-selectie: We gebruikten SHAP-waarden om kwantitatief sleutelkenmerken te identificeren en selecteerden 14 kritieke parameters die de diagnosebeslissing domineren.
- Classificatiediagnose: Met behulp van deze fysiek verrijkte dataset trainden we een Random Forest (RF) classificator en bereikten we een zeer nauwkeurige foutdiagnose.
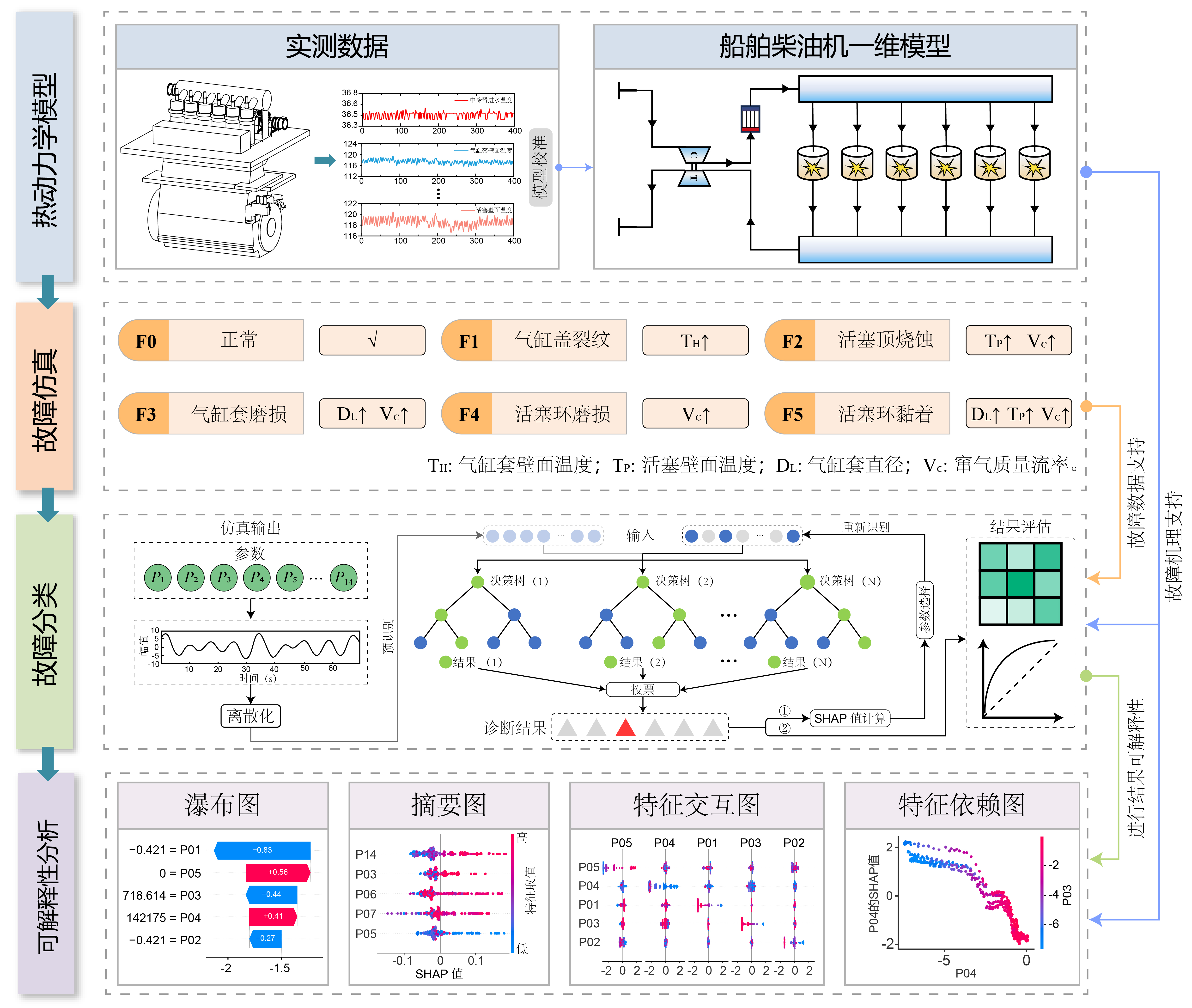
Afb. 1: Architectuur van de TSRF-methode.
Details Thermodynamische Modellering
Om een hoge getrouwheid te garanderen, hebben we een eendimensionaal dieselmotorsimulatiemodel gebouwd. Dit mechanistische model vindt een balans tussen fysieke nauwkeurigheid en de rekenkundige efficiëntie die nodig is voor datasetgeneratie.
Modeltopologie
Het motorsysteem is gediscretiseerd als een netwerk van vloeistofleidingen en functionele componenten:
- Kernkrachtbron: Lijnconfiguratie, zes cilinders, tweetakt.
- Luchtsysteem: Inlaat-/uitlaatspruitstukken (PL1, PL2) zijn verbonden via een complex leidingnetwerk.
- Drukvullingssysteem: Turbolader (TC1) gekoppeld aan intercooler (CO1).
Kalibratie en Validatie
Voordat de foutinjectie werd uitgevoerd, werd het basismodel rigoureus gekalibreerd op basis van gemeten data.
- Databron: Echte operationele scheepsdata verkregen via de Data Acquisition Module (DCM).
- Validatie: Afwijkingen van sleutelparameters (zoals vermogen, uitlaattemperatuur) werden strikt binnen een foutmarge van ±5% gehouden.
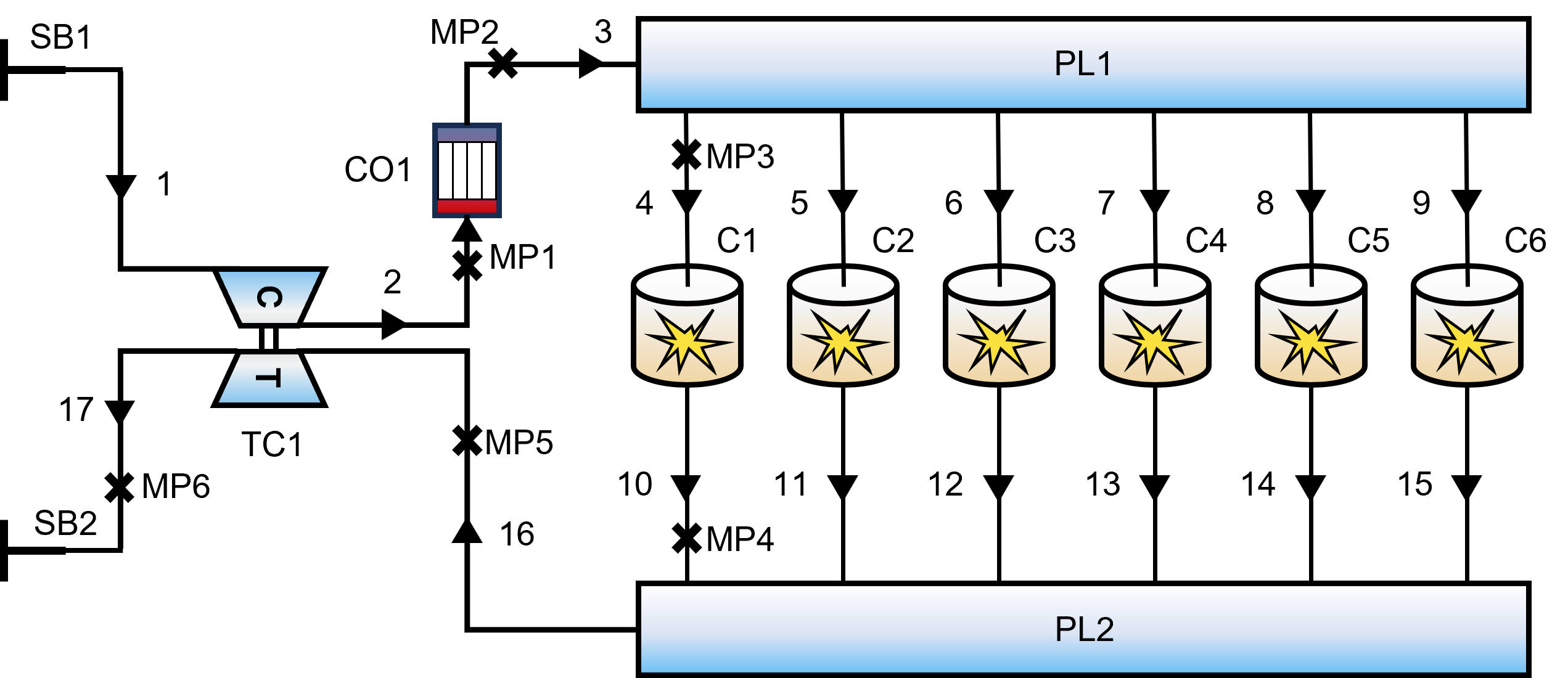
Afb. 2: Schema van het eendimensionale thermodynamische model van de dieselmotor.
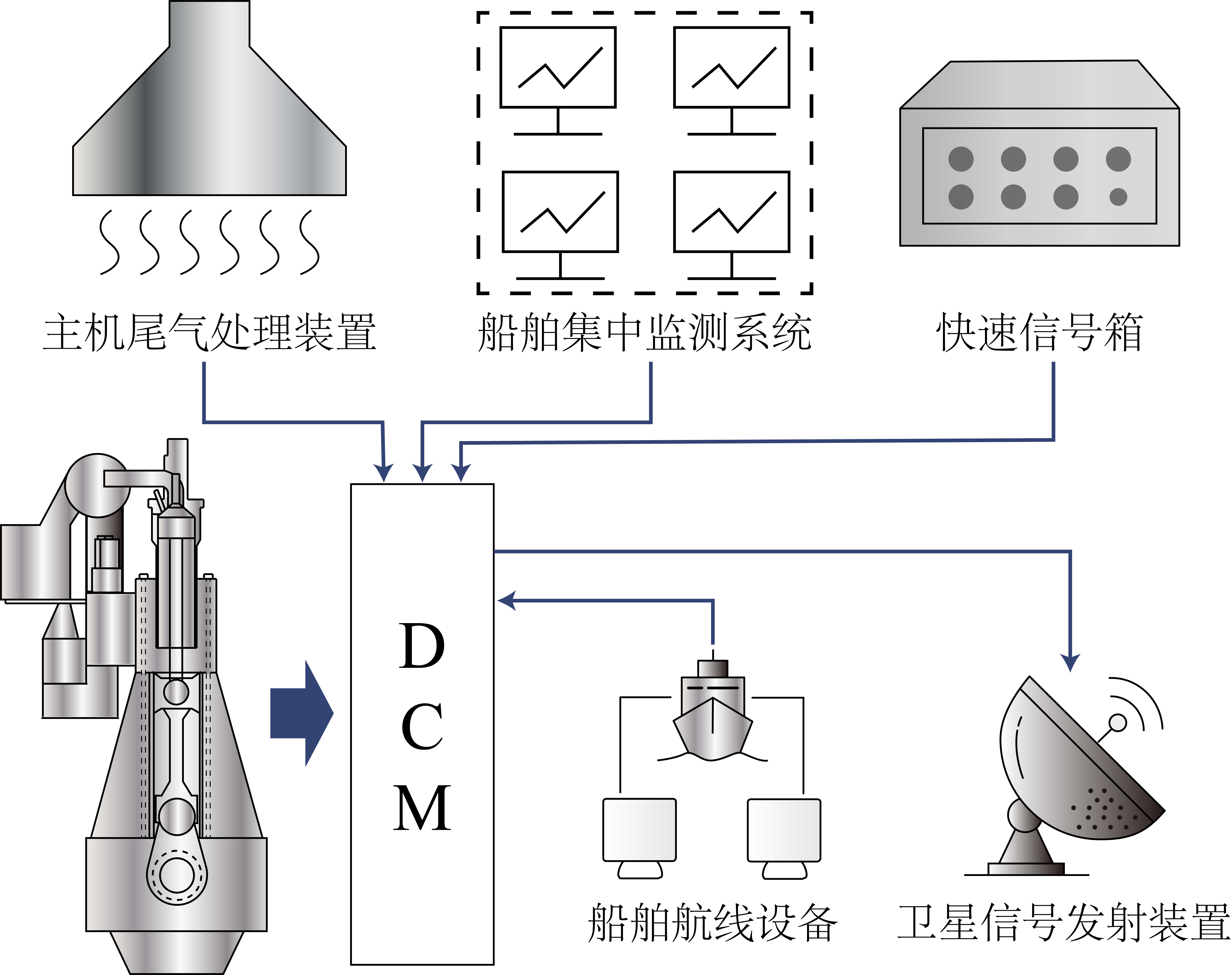
Afb. 5: Data Acquisition Module (DCM).
Foutinjectiemechanisme
Aangezien eendimensionale modellen 3D-structurele defecten niet direct kunnen weergeven, hebben we een fenomenologische mappingmethode toegepast om fysieke degradatiemechanismen te vertalen naar equivalente verschuivingen in thermodynamische parameters.
| Fouttype | Fysisch mechanisme | Modelleringsimplementatie |
|---|---|---|
| F1: Cilinderkopscheur | Belemmerde warmtegeleiding. | Verhogen van de oppervlaktetemperatuur van de cilinderkop ($T_H$) tot 346°C. |
| F2: Zuigerablatie | Materiaalverlies en afdichtingsfalen. | Verhogen van zuigertemperatuur ($T_P$) + lichte blow-by (0,01 kg/s). |
| F3: Voering (Liner) Slijtage | Vergroting van de boringdiameter door slijtage. | Vergroting van boring + ernstige blow-by (0,03 kg/s). |
| F4: Zuigerveer Slijtage | Gaslekkage. | Aanpassen van massastroom blow-by (0,02 kg/s). |
| F5: Zuigerveer Kleven | Toegenomen wrijving en afdichtingsfalen. | Verandering in boringdiameter + verhoging van voeringtemperatuur + blow-by. |
Verkalaringsanalyse
Een kerninnovatie van deze studie ligt in het verschuiven van de focus van "Wat is de fout?" naar "Waarom is deze fout gediagnosticeerd?". We demonstreerden dit vermogen door de analyse van zuigerveerslijtage (F4):
- Lokale Verklaring (Watervalplot): De watervalplot ontleedt de specifieke voorspellingslogica. Het model voorspelde bijvoorbeeld "zuigerveerslijtage" omdat de blow-by warmtestroom (P06) en blow-by massastroom (P07) specifieke waarden vertoonden, wat de voorspellingskans van deze fout verhoogde. Dit is consistent met natuurkundige wetten: zuigerveerslijtage vernietigt de afdichting, wat leidt tot gaslekkage (blow-by).
- Globale Verklaring (Beeswarmplot): De globale analyse onthult de algemene wetten die door het model zijn geleerd. We ontdekten dat een lage uitlaatdruk vóór de turbine (P11) een sterke indicator is voor zuigerveerslijtage. Fysisch gezien is dit consistent: versleten ringen leiden tot gaslekkage uit de cilinder, waardoor de beschikbare energie om de turbine aan te drijven afneemt.
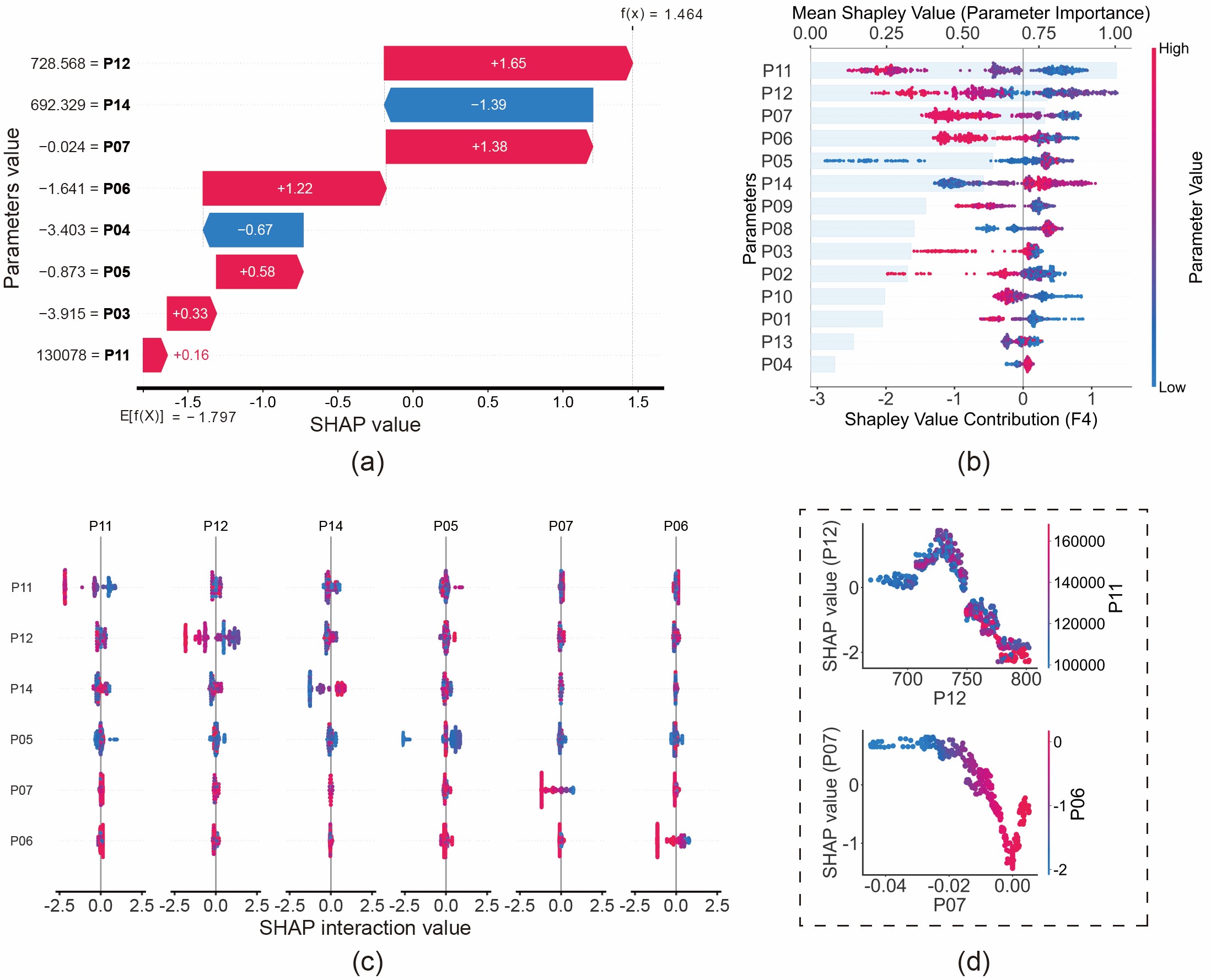
Afb. 11: Foutanalyse van zuigerveerslijtage (F4) op basis van SHAP-waarden: (a) Watervalplot; (b) Beeswarmplot; (c) Interactieplot; (d) Afhankelijkheidsplot.
Bekijk SHAP-visualisatiecode (Python)
Als u geïnteresseerd bent in de implementatiedetails van de bovenstaande grafieken, is hier voorbeeldcode voor het genereren van waterval-, beeswarm-, interactie- en afhankelijkheidsplots.👇
Onderzoekshoogtepunten
Wij geloven dat dit werk de volgende belangrijke bijdragen aan het veld heeft geleverd:
- Opzetten van geparametriseerde modellen voor vijf typische fouten van verbrandingskamercomponenten van scheepsdieselmotoren.
- Valideren van de effectiviteit van de SHAP-methode door vergelijking met meerdere feature-selectiemethoden.
- Bieden van een nieuw perspectief voor verklaarbare foutdiagnose door data-gedreven methoden te combineren met thermodynamische mechanistische modellen.