מוטיבציה למחקר
בתחום ההנדסה הימית וניהול פרוגנוסטיקה ובריאות (PHM), התעשייה מתמודדת עם שני צווארי בקבוק ארוכי טווח:
- מחסור בנתונים: מנועי דיזל ימיים (במיוחד מנועים ראשיים של ספינות אוקיינוס) הם לב הספינה. תקלה חמורה בים עלולה להוביל לאובדן כוח הנעה, עלייה על שרטון או אפילו אסון ימי. לכן, מקדמי הבטיחות בתכנון שלהם גבוהים במיוחד, וההסתברות לתקלות חמורות נמוכה מעצם טבעה. בנוסף, התעשייה הימית מיישמת מערכות תחזוקה מונעת קפדניות (כגון שיפוץ מתוזמן לפי שעות עבודה). הרוב המכריע של החלקים המתכלים מוחלפים בכפייה לפני שהם באמת כושלים ומייצרים נתוני תקלה. זה מוביל לשפע של נתוני בריאות ונתוני בלאי מוקדם, אך למחסור קיצוני בנתונים אמיתיים על כשל מלא או תקלות חמורות.
- בעיית "הקופסה השחורה": מכיוון שמודלים של למידה עמוקה חסרים בדרך כלל שקיפות, קשה למהנדסים לסמוך עליהם אם אינם יכולים להסביר את הסיבות הפיזיקליות לתקלה. בתעשיית הספנות, המפוקחת בקפדנות על ידי חברות סיווג, חוסר שקיפות זה הוא קריטי. אם בינה מלאכותית מאבחנת בטעות (או מפספסת) תפיסת בוכנה (scuffing) או שבר בגל הארכובה, והמערכת לא יכולה לעקוב אם השגיאה נובעת מהטיית נתונים, פגם באלגוריתם או סחיפת חיישן, חוסר עקיבות זה אינו מתקבל על הדעת בחקירות תאונות ימיות.
כדי להתמודד עם אתגרים אלו, הצענו את שיטת TSRF. על ידי מיזוג מודלים מכניסטיים מבוססי-פיזיקה עם טכניקות הסבר מתקדמות ושימוש במודלים של סימולציה בנאמנות גבוהה כדי לפתור את בעיית המחסור בנתונים, אנו מבטיחים שהחלטות האבחון תואמות לעקרונות תרמודינמיים בסיסיים.
מתודולוגיה
זרימת העבודה של מחקר זה כוללת את ארבעת השלבים העיקריים הבאים (כפי שמוצג באיור):
- מודלים תרמודינמיים: במקום להסתמך רק על ספסלי ניסוי פיזיים, בנינו מודל תרמודינמי חד-ממדי בנאמנות גבוהה של מנוע דיזל ימי בעל שישה צילינדרים. המודל כויל בקפדנות על סמך נתוני הפעלה אמיתיים, תוך שמירה על שגיאת סימולציה מתחת ל-5%.
- הזרקת תקלות: בהתבסס על המודל המכויל, דימינו חמש תקלות ספציפיות בתא הבעירה (כגון סדקים בראש הצילינדר, אבלציה של הבוכנה וכו') על ידי כוונון עדין של פרמטרים פיזיקליים, ובכך יצרנו סט נתונים המכסה דרגות שונות של תקלות מנוע אמיתיות.
- בחירת מאפיינים מבוססת SHAP: השתמשנו בערכי SHAP כדי לזהות באופן כמותי תכונות מפתח, ובחרנו 14 פרמטרים קריטיים השולטים בהחלטת האבחון.
- אבחון סיווג: באמצעות סט נתונים זה המועשר פיזיקלית, אימנו מסווג יער אקראי (RF) והשגנו אבחון תקלות ברמת דיוק גבוהה.
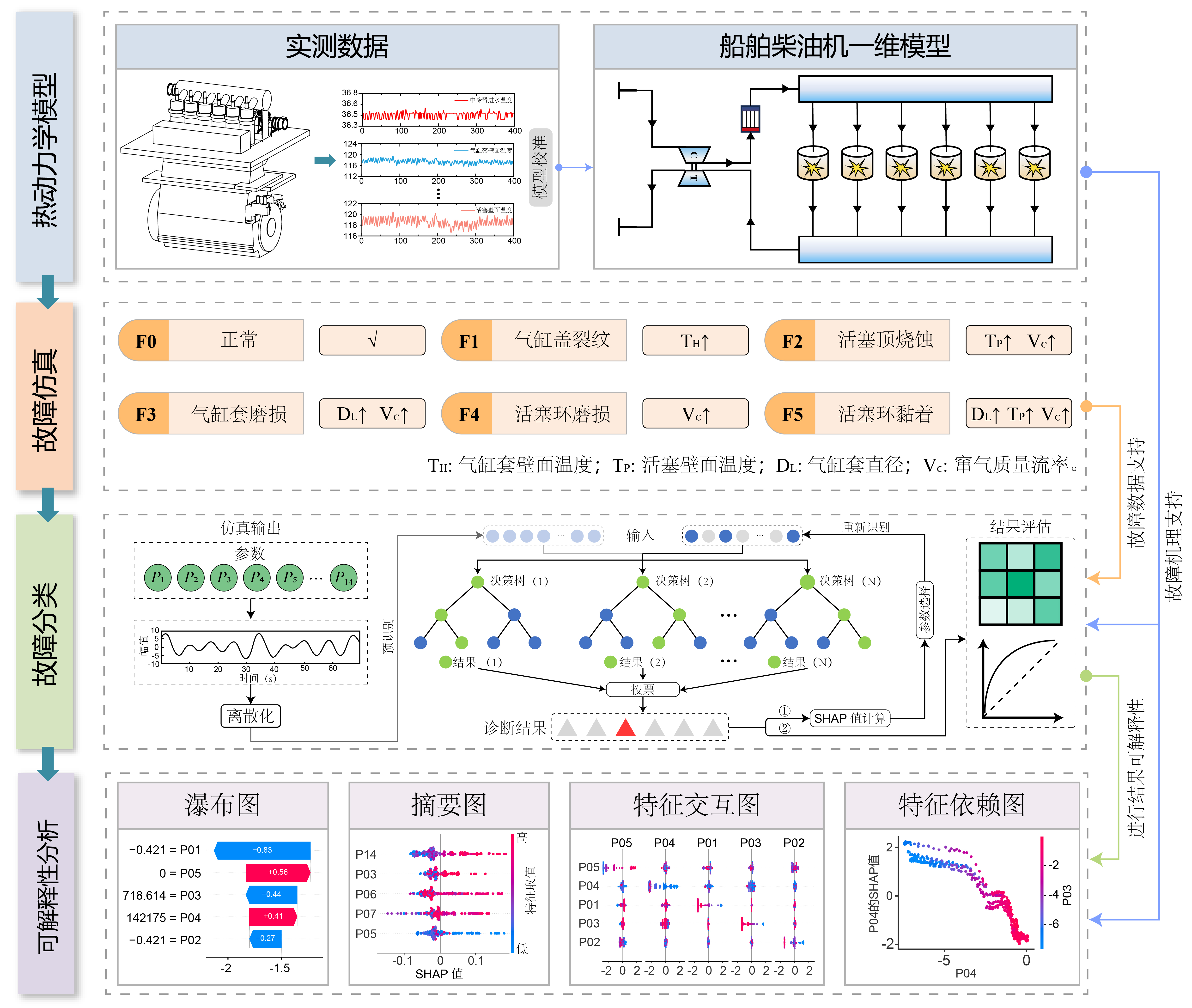
איור 1: ארכיטקטורת שיטת TSRF.
פרטי המידול התרמודינמי
כדי להבטיח נאמנות גבוהה, בנינו מודל סימולציה של מנוע דיזל חד-ממדי. מודל מכניסטי זה מאזן בין דיוק פיזיקלי ליעילות חישובית הנדרשת ליצירת סט הנתונים.
טופולוגיית המודל
מערכת המנוע מתוארת כרשת של צינורות נוזל ורכיבים פונקציונליים:
- יחידת כוח ליבה: תצורת שורה, שישה צילינדרים, שתי פעימות.
- מערכת אוויר: סעפות יניקה/פליטה (PL1, PL2) מחוברות באמצעות רשת צנרת מורכבת.
- מערכת גדישה: מגדש טורבו (TC1) מצומד למצנן ביניים (CO1).
כיול ואימות
לפני ביצוע הזרקת התקלות, המודל הבסיסי כויל בקפדנות על סמך נתונים מדודים.
- מקור נתונים: נתוני הפעלה אמיתיים של הספינה שנרכשו באמצעות מודול איסוף הנתונים (DCM).
- אימות: סטירות של פרמטרים מרכזיים (כגון כוח, טמפרטורת פליטה) נשלטו בקפדנות בתוך טווח שגיאה של ±5% .
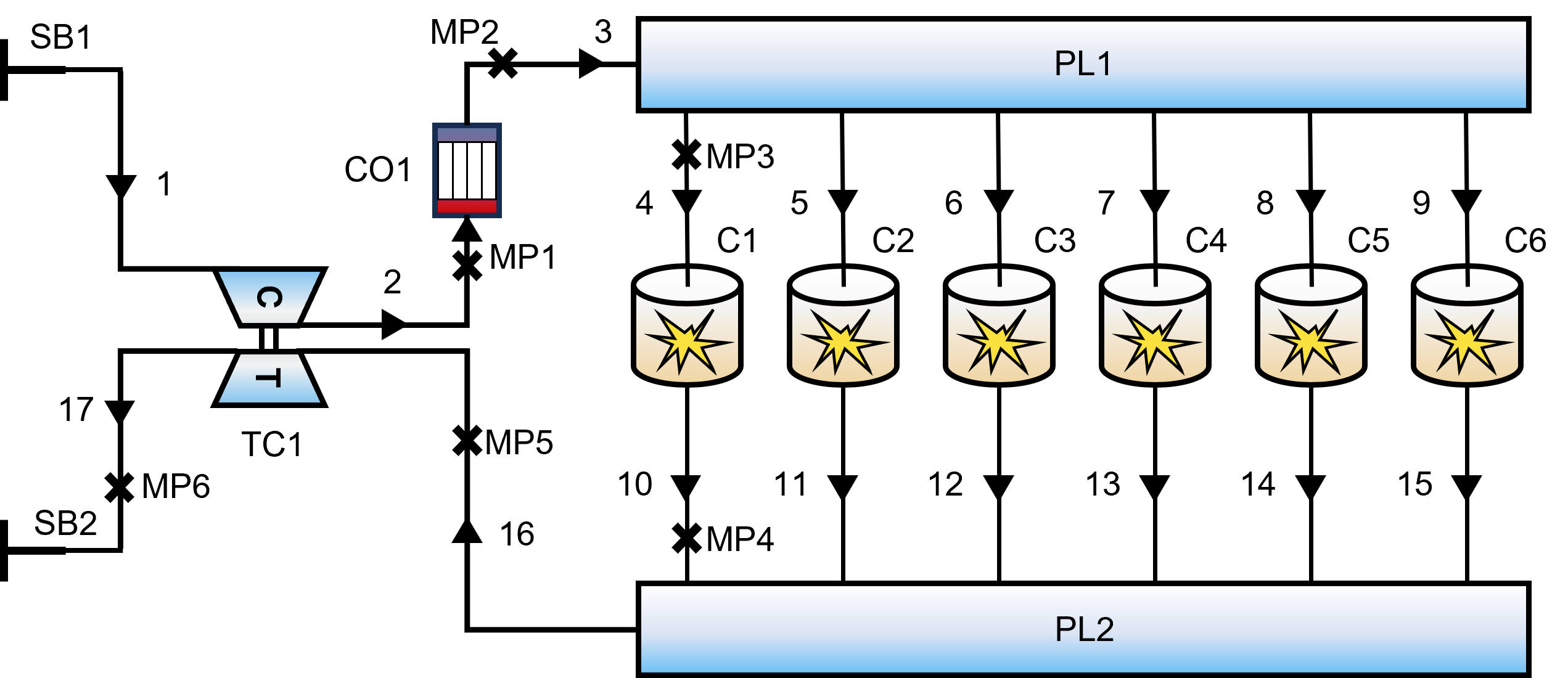
איור 2: סכמה של המודל התרמודינמי החד-ממדי של מנוע הדיזל.
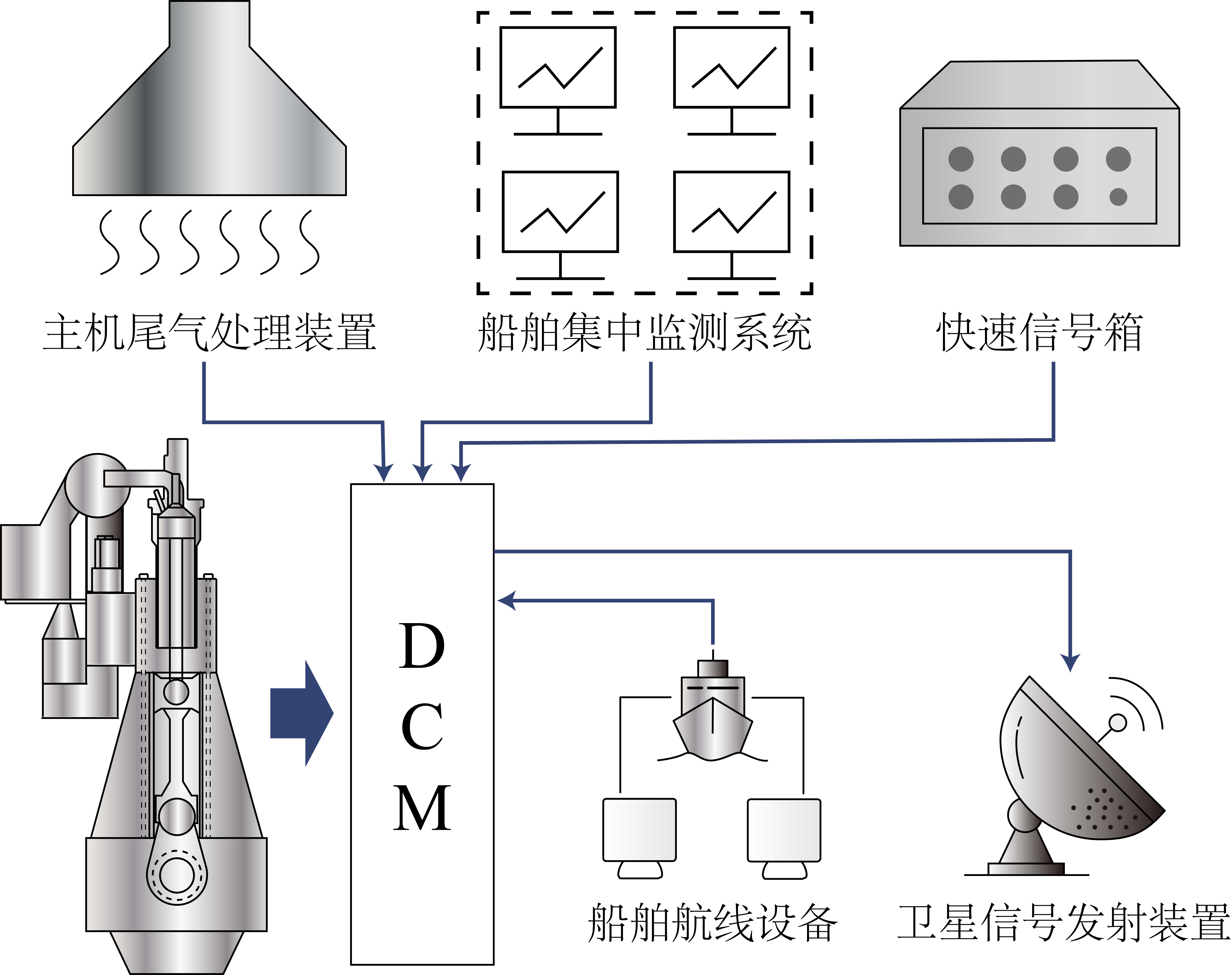
איור 5: מודול איסוף נתונים (DCM).
מנגנון הזרקת תקלות
מכיוון שמודלים חד-ממדיים אינם יכולים לייצג ישירות פגמים מבניים תלת-ממדיים, אימצנו שיטת מיפוי פנומנולוגית כדי לתרגם מנגנוני התדרדרות פיזיקליים להזזות שוות ערך של פרמטרים תרמודינמיים.
| סוג תקלה | מנגנון פיזיקלי | יישום במודל |
|---|---|---|
| F1: סדק בראש הצילינדר | הולכת חום מופרעת. | העלאת טמפרטורת פני השטח של ראש הצילינדר ($T_H$) ל-346°C. |
| F2: אבלציה של הבוכנה | אובדן חומר וכשל באיטום. | העלאת טמפרטורת הבוכנה ($T_P$) + דליפת גזים (Blow-by) קלה (0.01 ק"ג/שנייה). |
| F3: שחיקת שרוול (Liner) | הגדלת הקדח עקב שחיקה. | הגדלת הקדח + דליפת גזים חמורה (0.03 ק"ג/שנייה). |
| F4: שחיקת טבעות | דליפת גז. | התאמת קצב זרימת המסה של דליפת הגזים (0.02 ק"ג/שנייה). |
| F5: היתפסות טבעות | חיכוך מוגבר וכשל באיטום. | שינוי קוטר הקדח + עליית טמפרטורת השרוול + דליפת גזים. |
ניתוח יכולת ההסבר
חידוש מרכזי במחקר זה טמון בהסטת המיקוד מ"מהי התקלה?" ל"מדוע אובחנה תקלה זו?". הדגמנו יכולת זו באמצעות ניתוח שחיקת טבעות הבוכנה (F4):
- הסבר מקומי (גרף מפל): גרף המפל מפרק את לוגיקת החיזוי הספציפית. למשל, המודל חזה "שחיקת טבעות" משום ששטף החום של דליפת הגזים (P06) וקצב זרימת המסה של דליפת הגזים (P07) הציגו ערכים ספציפיים, ובכך העלו את הסתברות החיזוי לתקלה זו. זה עולה בקנה אחד עם החוקים הפיזיקליים: שחיקת טבעות הורסת את האיטום, ומובילה לדליפת גז (Blow-by).
- הסבר גלובלי (גרף נחיל דבורים): הניתוח הגלובלי חושף את החוקים הכלליים שנלמדו על ידי המודל. מצאנו כי ערך נמוך של לחץ פליטה לפני הטורבינה (P11) הוא אינדיקטור חזק לשחיקת טבעות. מבחינה פיזיקלית, זה עקבי: טבעות שחוקות גורמות לדליפת גז מהצילינדר, ובכך מפחיתות את האנרגיה הזמינה להנעת הטורבינה.
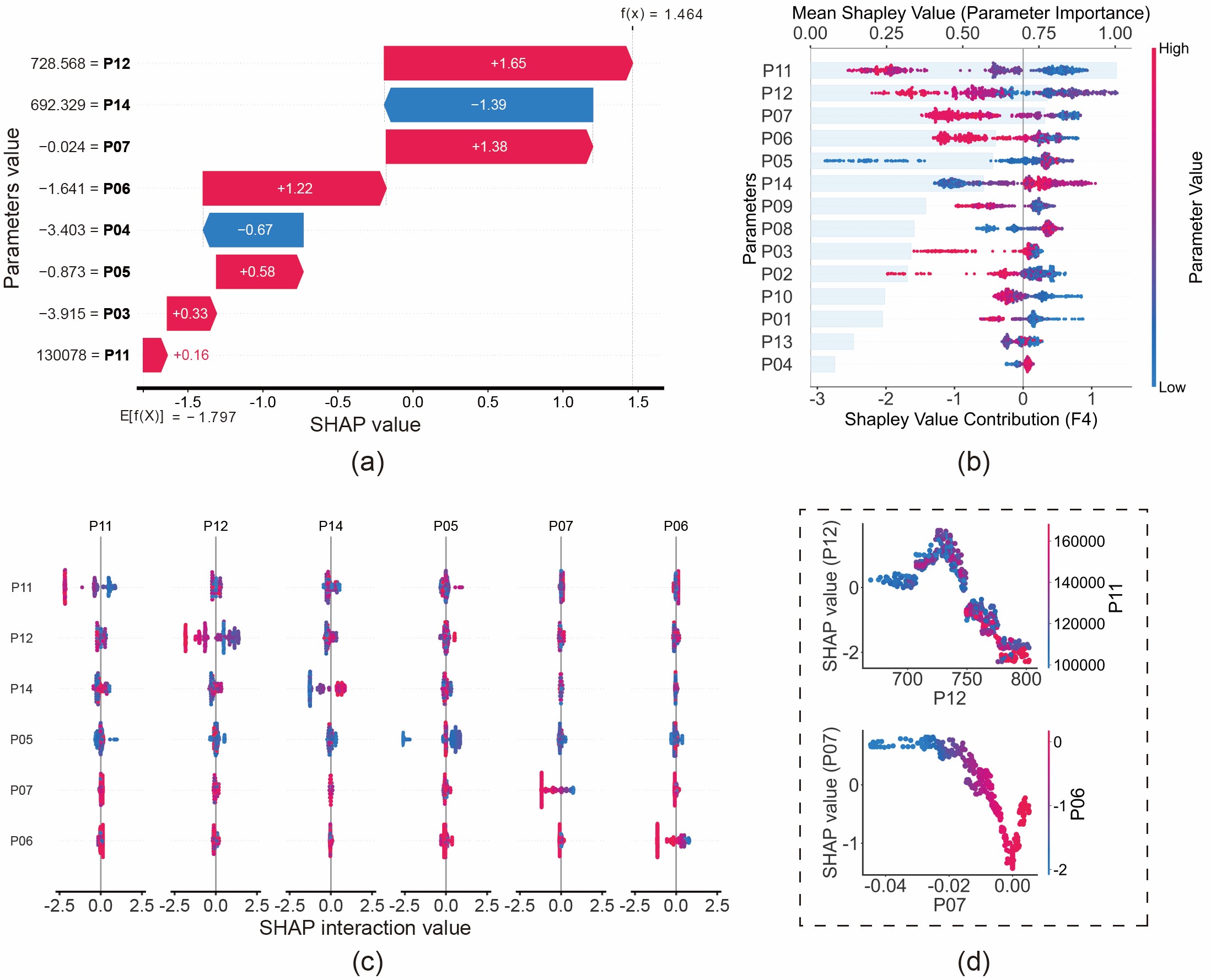
איור 11: ניתוח תקלת שחיקת טבעות (F4) מבוסס ערכי SHAP: (א) גרף מפל; (ב) גרף נחיל דבורים; (ג) גרף אינטראקציה; (ד) גרף תלות.
הצג קוד ויזואליזציה של SHAP (Python)
אם אתם מעוניינים בפרטי היישום של הגרפים לעיל, הנה קוד לדוגמה ליצירת גרפי מפל, נחיל, אינטראקציה ותלות.👇
נקודות עיקריות במחקר
אנו מאמינים כי עבודה זו תרמה את התרומות המרכזיות הבאות לתחום:
- ביסוס מודלים פרמטריים לחמש תקלות אופייניות של רכיבי תא הבעירה במנועי דיזל ימיים.
- אימות היעילות של שיטת SHAP באמצעות השוואה למספר שיטות לבחירת מאפיינים.
- מתן פרספקטיבה חדשה לאבחון תקלות מוסבר על ידי מיזוג שיטות מונחות-נתונים עם מודלים מכניסטיים תרמודינמיים.