Motivation
Im Bereich der Meerestechnik und des Prognostics and Health Management (PHM) steht die Industrie vor zwei langfristigen Engpässen:
- Datenknappheit: Schiffsdieselmotoren (insbesondere Hauptmaschinen von Hochseeschiffen) sind das Herzstück des Schiffes. Ein schwerwiegender Ausfall auf See kann zu Antriebsverlust, Strandung oder sogar Katastrophen führen. Daher sind ihre Sicherheitsfaktoren bei der Konstruktion extrem hoch, und die Wahrscheinlichkeit schwerwiegender Fehler ist an sich sehr gering. Zudem führt die Schifffahrtsindustrie strenge vorbeugende Wartungssysteme durch (z. B. zeitbasierte Überholung nach Betriebsstunden). Die überwiegende Mehrheit der Verschleißteile wird zwangsweise ausgetauscht, bevor sie tatsächlich ausfallen und Fehlerdaten generieren. Dies führt dazu, dass zwar große Mengen an Gesundheitsdaten und Daten zu frühem Verschleiß vorhanden sind, aber echte Daten zu vollständigem Ausfall oder schweren Fehlern extrem fehlen.
- Das „Black-Box“-Problem: Da Deep-Learning-Modelle in der Regel intransparent sind, fällt es Ingenieuren schwer, ihnen zu vertrauen, wenn die physikalischen Ursachen eines Fehlers nicht erklärt werden können. In der streng regulierten Schifffahrtsindustrie (durch Klassifikationsgesellschaften) ist diese Intransparenz besonders kritisch. Wenn eine KI fälschlicherweise einen Kolbenfresser oder Kurbelwellenbruch prognostiziert (oder übersieht) und das System nicht nachvollziehen kann, ob der Fehler auf Datenverzerrung, Algorithmusmängel oder Sensordrift zurückzuführen ist, ist dies bei der Untersuchung von Seeunfällen inakzeptabel.
Um diesen Herausforderungen zu begegnen, haben wir die TSRF-Methode vorgeschlagen. Durch die Fusion von physikbasierten mechanistischen Modellen mit fortschrittlichen Techniken der Erklärbarkeit und der Nutzung von High-Fidelity-Simulationsmodellen lösen wir das Problem der Datenknappheit und stellen sicher, dass Diagnoseentscheidungen den thermodynamischen Grundprinzipien entsprechen.
Methodik
Der Arbeitsablauf dieser Studie umfasst die folgenden vier Hauptphasen (siehe Abbildung):
- Thermodynamische Modellierung: Anstatt uns ausschließlich auf physische Prüfstände zu verlassen, haben wir ein hochgenaues eindimensionales thermodynamisches Modell eines Sechszylinder-Schiffsdieselmotors erstellt. Das Modell wurde streng auf Basis realer Betriebsdaten kalibriert, wobei der Simulationsfehler unter 5 % gehalten wurde.
- Fehlerinjizierung: Basierend auf dem kalibrierten Modell simulierten wir fünf spezifische Brennraumfehler (z. B. Zylinderkopfrisse, Kolbenabbrand), indem wir physikalische Parameter feinjustierten, um einen Datensatz zu generieren, der verschiedene Schweregrade realer Motorfehler abdeckt.
- SHAP-basierte Merkmalsselektion: Wir nutzten SHAP-Werte, um Schlüsselmerkmale quantitativ zu identifizieren und 14 kritische Parameter auszuwählen, die die Diagnoseentscheidung dominieren.
- Klassifikation und Diagnose: Unter Verwendung dieses physikalisch erweiterten Datensatzes trainierten wir einen Random Forest (RF) Klassifikator und erzielten eine hochpräzise Fehlerdiagnose.
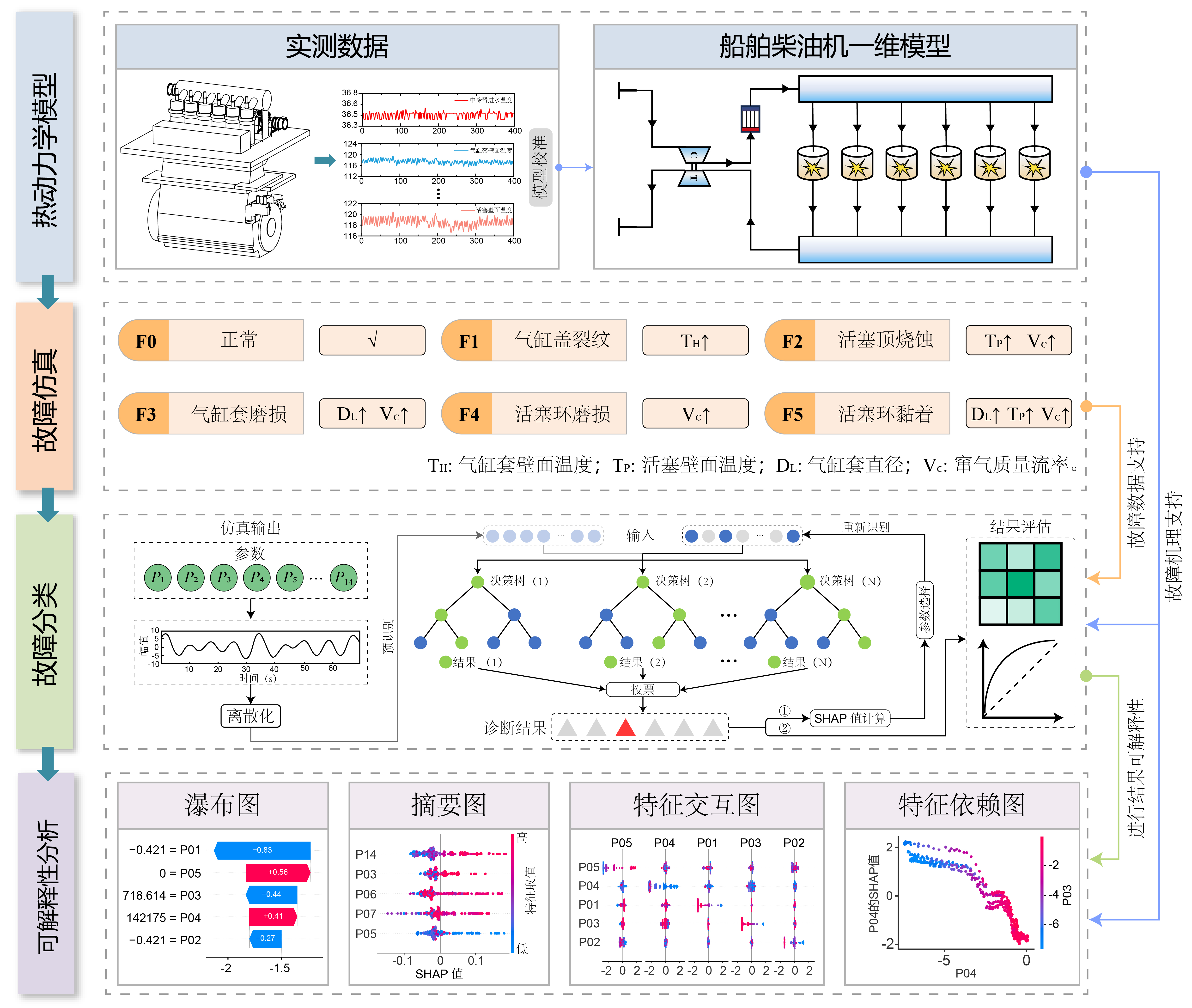
Abb. 1: Architektur der TSRF-Methode.
Details zur thermodynamischen Modellierung
Um eine hohe Wiedergabetreue zu gewährleisten, haben wir ein eindimensionales Dieselsimulationsmodell erstellt. Dieses mechanistische Modell hält die Balance zwischen physikalischer Genauigkeit und der für die Datensatzgenerierung erforderlichen Recheneffizienz.
Modelltopologie
Das Motorsystem wird als Netzwerk aus Fluidleitungen und Funktionskomponenten diskretisiert:
- Kernantriebseinheit: Sechszylinder, Zweitakt-Reihenanordnung.
- Gassystem: Ein-/Auslasskrümmer (PL1, PL2) sind über ein komplexes Rohrleitungsnetz verbunden.
- Aufladesystem: Turbolader (TC1) gekoppelt mit Ladeluftkühler (CO1).
Kalibrierung und Validierung
Vor der Fehlerinjizierung wurde das Basismodell anhand von Messdaten streng kalibriert.
- Datenquelle: Reale Schiffsbetriebsdaten, erfasst über das Datenerfassungsmodul (DCM).
- Validierung: Abweichungen wichtiger Parameter (wie Leistung, Abgastemperatur) wurden streng innerhalb eines Fehlerbereichs von ±5% gehalten.
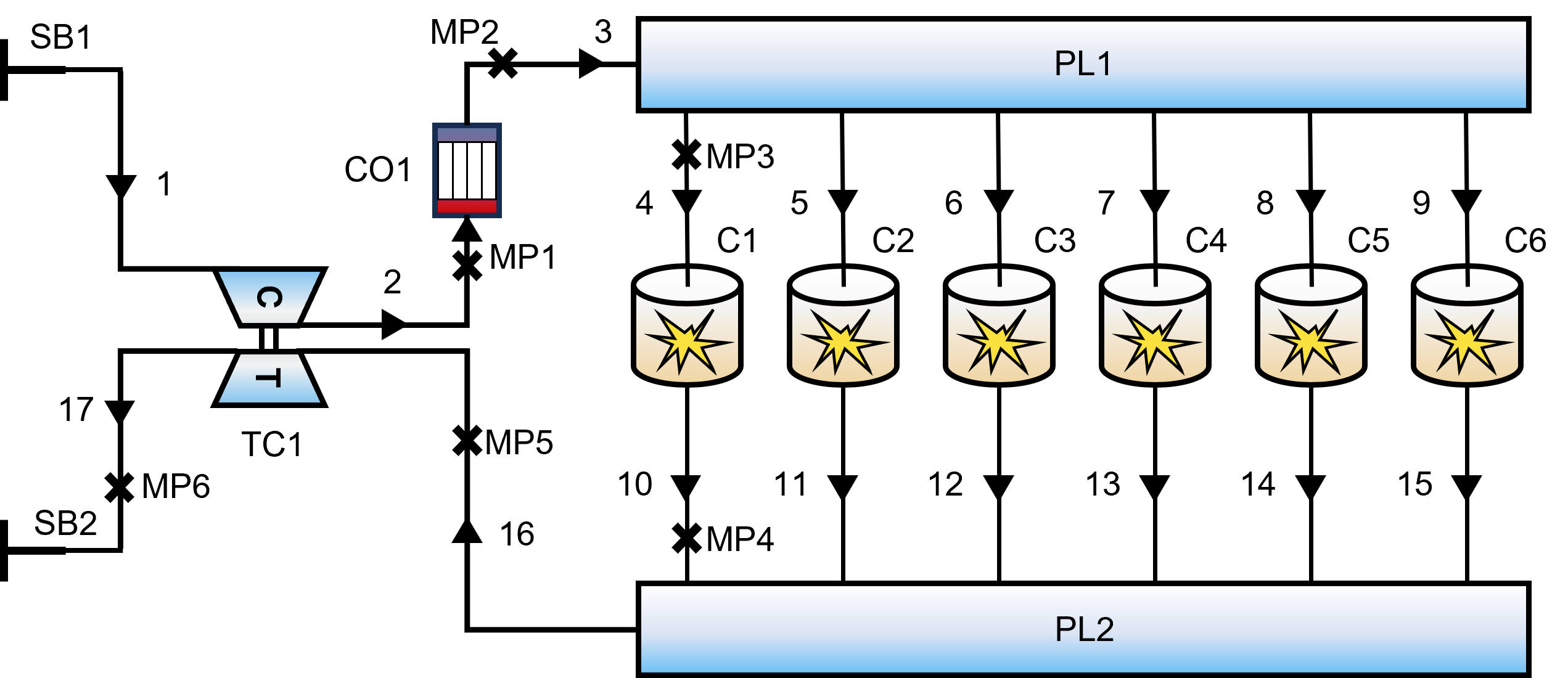
Abb. 2: Schematische Darstellung des eindimensionalen thermodynamischen Modells des Dieselmotors.
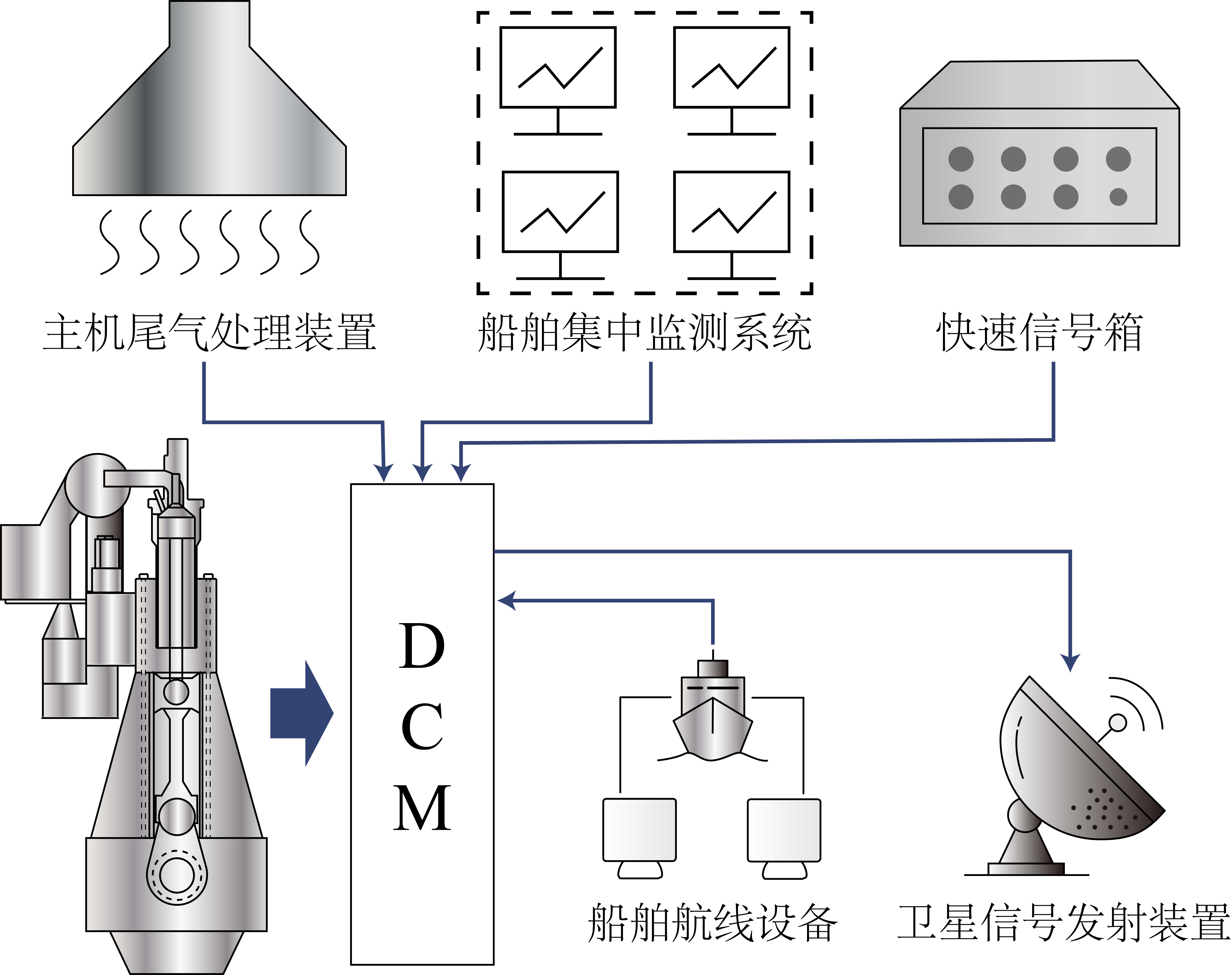
Abb. 5: Datenerfassungsmodul (DCM).
Mechanismus der Fehlerinjizierung
Da eindimensionale Modelle 3D-Strukturdefekte nicht direkt darstellen können, verwendeten wir eine phänomenologische Abbildungsmethode, um physikalische Degradationsmechanismen in äquivalente thermodynamische Parameterverschiebungen umzuwandeln.
| Fehlertyp | Physikalischer Mechanismus | Modellierungsimplementierung |
|---|---|---|
| F1: Zylinderkopfriss | Behinderte Wärmeleitung. | Erhöhung der Zylinderkopfoberflächentemperatur ($T_H$) auf 346°C. |
| F2: Kolbenabbrand | Materialverlust und Dichtungsversagen. | Erhöhung der Kolbentemperatur ($T_P$) + leichtes Blow-by (0,01 kg/s). |
| F3: Laufbuchsenverschleiß | Vergrößerung des Bohrungsdurchmessers durch Verschleiß. | Vergrößerung der Bohrung + starkes Blow-by (0,03 kg/s). |
| F4: Kolbenringverschleiß | Gasaustritt. | Anpassung des Blow-by-Massenstroms (0,02 kg/s). |
| F5: Kolbenringklemmen | Erhöhte Reibung und Dichtungsversagen. | Änderung des Bohrungsdurchmessers + Erhöhung der Laufbuchsentemperatur + Blow-by. |
Analyse der Erklärbarkeit
Eine Kerninnovation dieser Studie besteht darin, den Fokus von „Was ist der Fehler?“ auf „Warum wurde dieser Fehler diagnostiziert?“ zu verlagern. Wir demonstrierten diese Fähigkeit anhand der Analyse des Kolbenringverschleißes (F4):
- Lokale Erklärung (Waterfall-Plot): Der Waterfall-Plot schlüsselt die spezifische Vorhersagelogik auf. Zum Beispiel prognostizierte das Modell „Kolbenringverschleiß“, weil der Blow-by-Wärmestrom (P06) und der Blow-by-Massenstrom (P07) spezifische Werte annahmen, was die Vorhersagewahrscheinlichkeit für diesen Fehler erhöhte. Dies stimmt mit den physikalischen Gesetzen überein: Kolbenringverschleiß zerstört die Abdichtung und führt zu Gasaustritt (Blow-by).
- Globale Erklärung (Beeswarm-Plot): Die globale Analyse offenbart die vom Modell erlernten allgemeinen Gesetze. Wir stellten fest, dass ein niedriger Abgasdruck vor der Turbine (P11) ein starker Indikator für Kolbenringverschleiß ist. Physikalisch ist dies konsistent: Verschlissene Kolbenringe führen zu Gasleckagen aus dem Zylinder, wodurch die verfügbare Energie zum Antrieb der Turbine verringert wird.
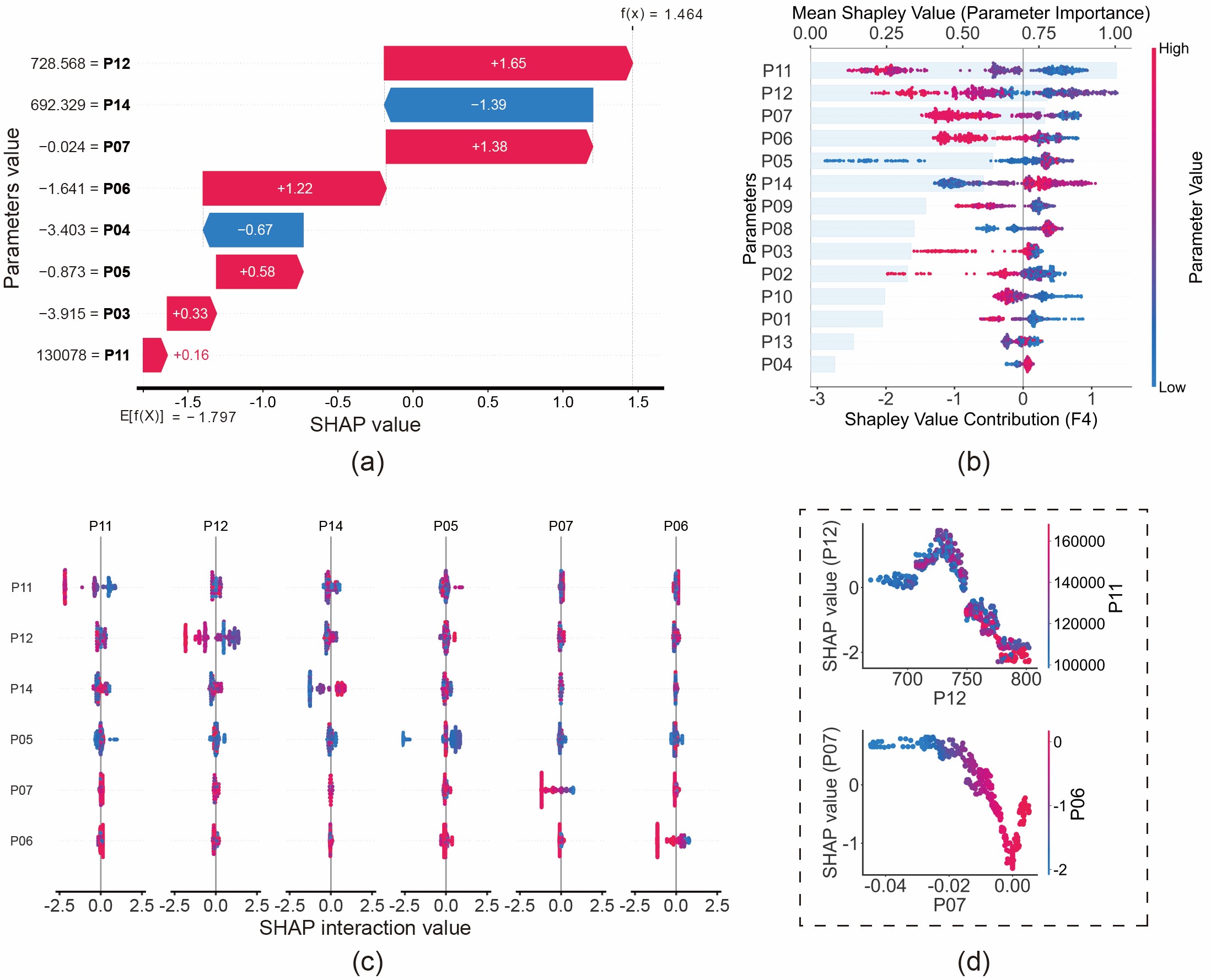
Abb. 11: Auf SHAP-Werten basierende Fehleranalyse für Kolbenringverschleiß (F4): (a) Waterfall-Plot; (b) Beeswarm-Plot; (c) Interaktionsdiagramm; (d) Abhängigkeitsdiagramm.
SHAP-Visualisierungscode anzeigen (Python)
Wenn Sie an den Implementierungsdetails der obigen Diagramme interessiert sind, finden Sie hier Beispielcode zur Generierung von Waterfall-, Beeswarm-, Interaktions- und Abhängigkeitsdiagrammen.👇
Forschungshighlights
Wir glauben, dass diese Arbeit folgende wichtige Beiträge zu diesem Bereich geleistet hat:
- Etablierung parametrisierter Modelle für fünf typische Fehler von Brennraumkomponenten in Schiffsdieselmotoren.
- Validierung der Wirksamkeit der SHAP-Methode durch Vergleich mit mehreren Merkmalsselektionsmethoden.
- Bereitstellung einer neuen Perspektive für erklärbare Fehlerdiagnose durch die Fusion datengetriebener Methoden mit thermodynamischen mechanistischen Modellen.