Motivace výzkumu
V oblasti námořního inženýrství a prognostiky a řízení stavu (PHM) čelí průmysl dvěma dlouhodobým úskalím:
- Nedostatek dat: Lodní dieselové motory (zejména hlavní motory zaoceánských lodí) jsou srdcem lodi. Vážná porucha na moři může vést ke ztrátě pohonu, uvíznutí nebo dokonce k námořní katastrofě. Proto jsou jejich bezpečnostní faktory při návrhu extrémně vysoké a pravděpodobnost vážných poruch je ze své podstaty velmi nízká. Námořní průmysl navíc uplatňuje přísné systémy preventivní údržby (např. plánované generální opravy podle provozních hodin). Naprostá většina opotřebitelných dílů je nuceně vyměněna dříve, než skutečně selže a vygeneruje data o poruše. To vede k nadbytku dat o bezporuchovém stavu a raném opotřebení, ale k extrémnímu nedostatku reálných dat o úplném selhání nebo vážných závadách.
- Problém "černé skříňky": Vzhledem k tomu, že modely hlubokého učení obvykle postrádají transparentnost, je pro inženýry obtížné jim důvěřovat, pokud nedokážou vysvětlit fyzikální příčiny poruchy. V lodním průmyslu, který je přísně regulován klasifikačními společnostmi, je tato netransparentnost kritická. Pokud AI chybně diagnostikuje (nebo přehlédne) zadírání pístu nebo prasknutí klikového hřídele a systém nedokáže zpětně vysledovat, zda chyba pramení ze zkreslení dat, vady algoritmu nebo driftu senzoru, je tato nemožnost zpětné vysledovatelnosti při vyšetřování námořních nehod nepřijatelná.
K řešení těchto výzev jsme navrhli metodu TSRF. Spojením fyzikálně založených mechanistických modelů s pokročilými technikami vysvětlitelnosti a využitím vysoce věrných simulačních modelů k řešení problému nedostatku dat zajišťujeme, že diagnostická rozhodnutí jsou v souladu se základními termodynamickými principy.
Metodika
Pracovní postup této studie zahrnuje následující čtyři hlavní fáze (jak je znázorněno na obrázku):
- Termodynamické modelování: Místo spoléhání se pouze na fyzické zkušební stolice jsme vytvořili vysoce věrný jednorozměrný termodynamický model šestiválcového lodního dieselového motoru. Model byl přísně kalibrován na základě skutečných provozních dat, přičemž chyba simulace byla udržena pod 5 %.
- Injektáž poruch: Na základě kalibrovaného modelu jsme simulovali pět specifických poruch spalovací komory (jako jsou praskliny hlavy válce, ablace pístu atd.) jemným doladěním fyzikálních parametrů, čímž jsme vytvořili datovou sadu pokrývající různé stupně skutečných poruch motoru.
- Výběr příznaků založený na SHAP: Použili jsme hodnoty SHAP ke kvantitativní identifikaci klíčových příznaků a vybrali 14 kritických parametrů, které dominují diagnostickému rozhodování.
- Klasifikační diagnostika: Pomocí této fyzikálně rozšířené datové sady jsme natrénovali klasifikátor náhodného lesa (RF) a dosáhli vysoce přesné diagnostiky poruch.
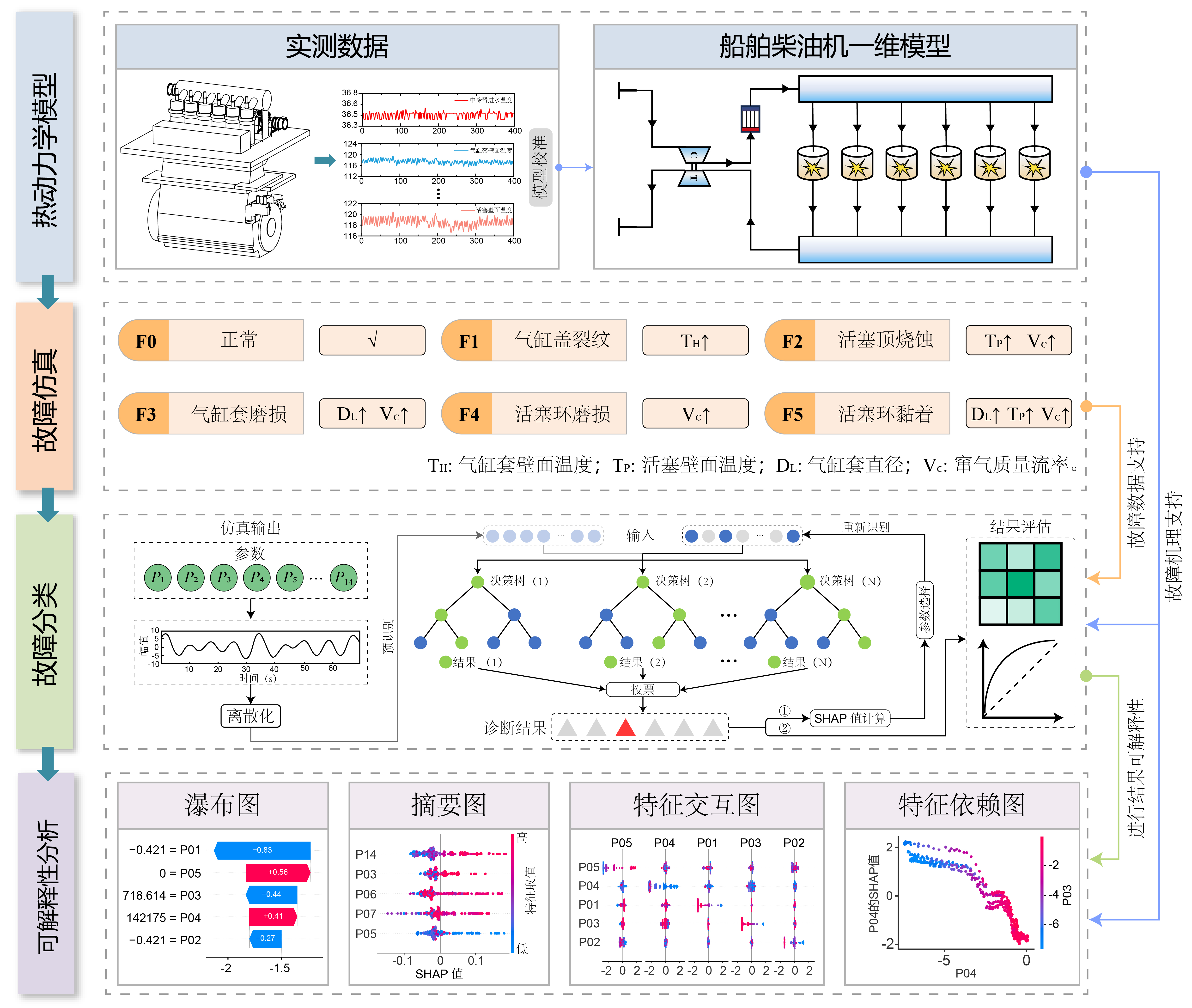
Obr. 1: Architektura metody TSRF.
Detaily termodynamického modelování
Pro zajištění vysoké věrnosti jsme vytvořili jednorozměrný simulační model dieselového motoru. Tento mechanistický model vyvažuje fyzikální přesnost a výpočetní efektivitu potřebnou pro generování datové sady.
Topologie modelu
Systém motoru je diskretizován jako síť kapalinových potrubí a funkčních komponent:
- Jádrová pohonná jednotka: Řadová konfigurace, šest válců, dvoutakt.
- Vzduchový systém: Sací/výfukové potrubí (PL1, PL2) je propojeno složitou sítí trubek.
- Přeplňovací systém: Turbodmychadlo (TC1) spojené s mezichladičem (CO1).
Kalibrace a validace
Před provedením injektáže poruch byl základní model přísně kalibrován na základě naměřených dat.
- Zdroj dat: Skutečná provozní data lodi získaná prostřednictvím modulu sběru dat (DCM).
- Validace: Odchylky klíčových parametrů (jako výkon, teplota výfukových plynů) byly přísně kontrolovány v rozmezí chyby ±5 % .
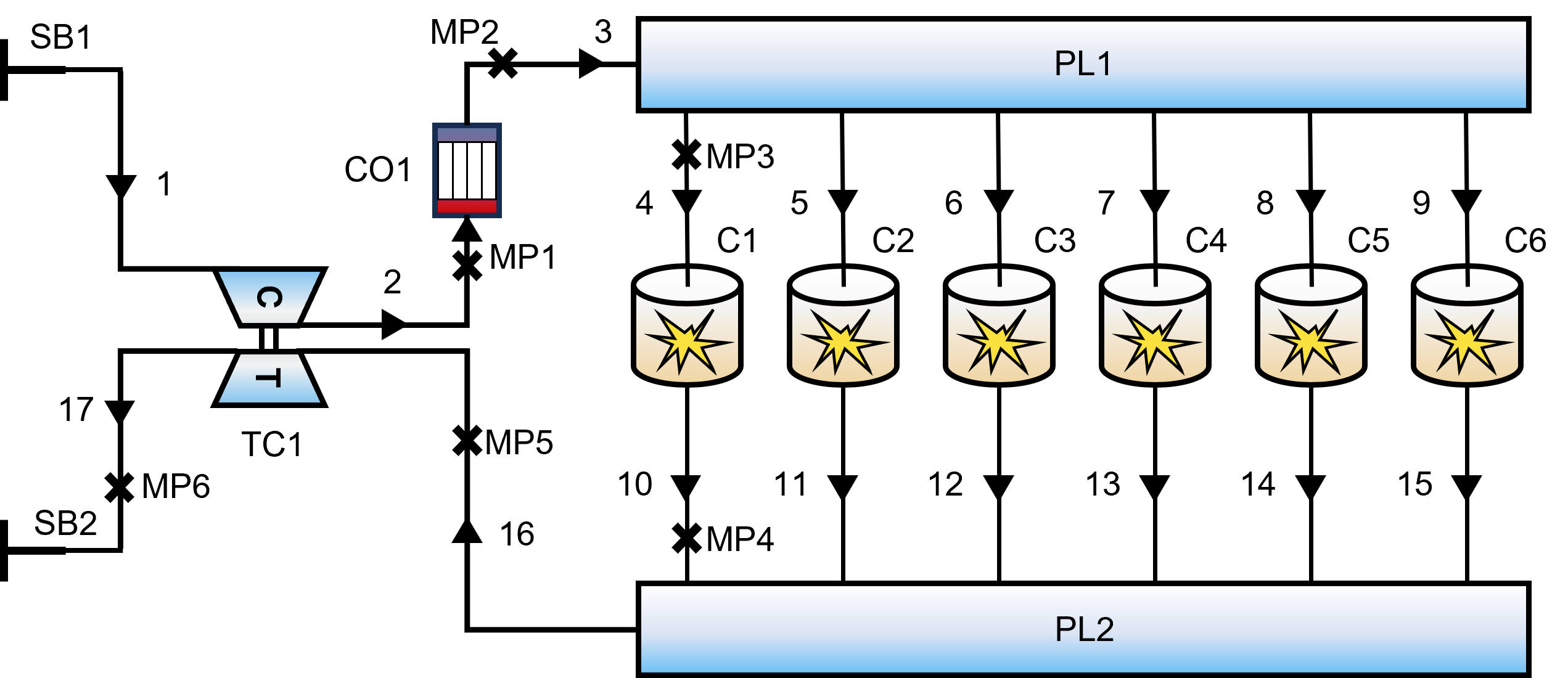
Obr. 2: Schéma jednorozměrného termodynamického modelu dieselového motoru.
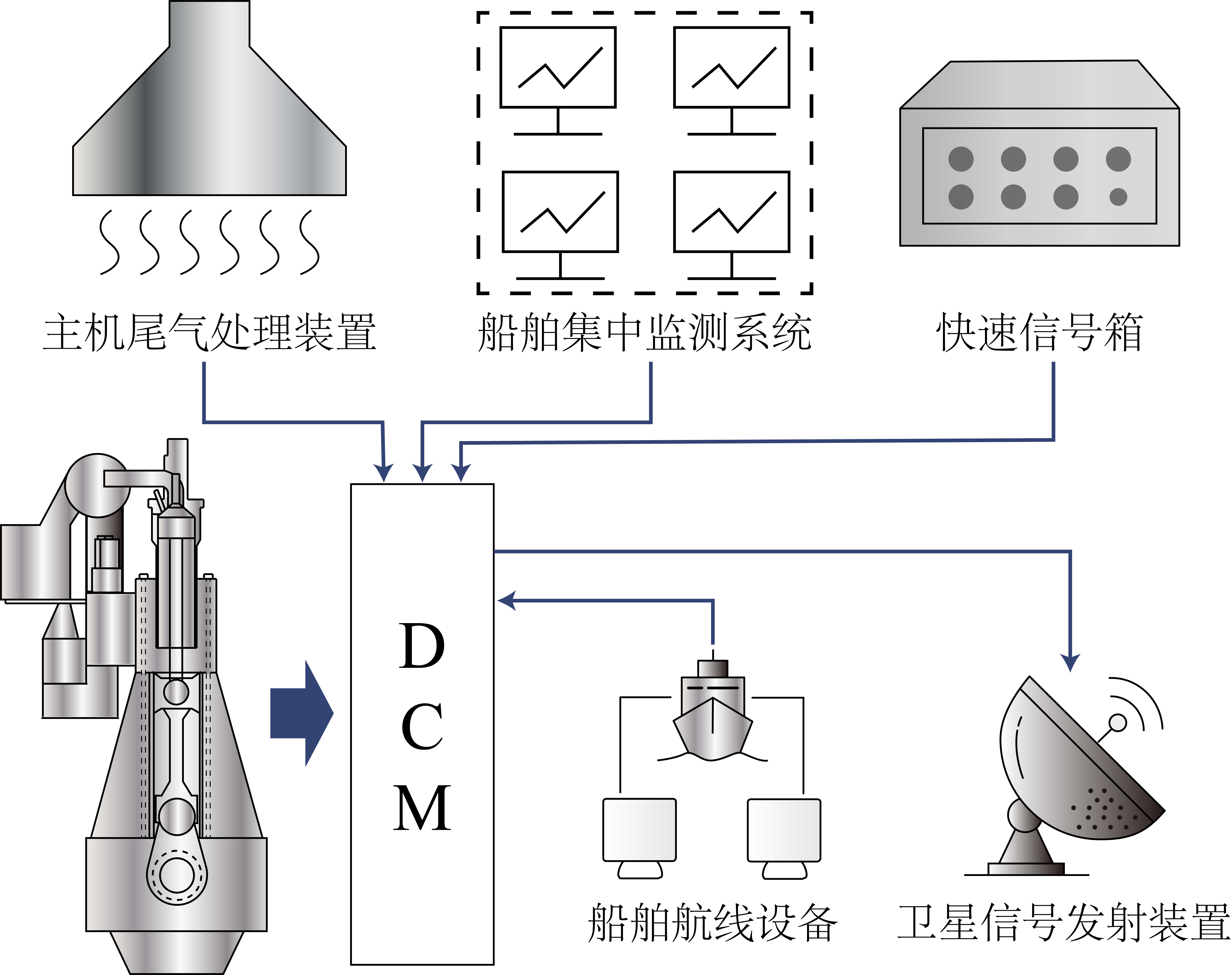
Obr. 5: Modul sběru dat (DCM).
Mechanismus injektáže poruch
Vzhledem k tomu, že jednorozměrné modely nemohou přímo reprezentovat 3D strukturální vady, přijali jsme metodu fenomenologického mapování pro převod mechanismů fyzikální degradace na ekvivalentní posuny termodynamických parametrů.
| Typ poruchy | Fyzikální mechanismus | Implementace modelování |
|---|---|---|
| F1: Prasklina hlavy válce | Omezené vedení tepla. | Zvýšení povrchové teploty hlavy válce ($T_H$) na 346 °C. |
| F2: Ablace pístu | Ztráta materiálu a selhání těsnění. | Zvýšení teploty pístu ($T_P$) + mírný profuk plynů (blow-by) (0,01 kg/s). |
| F3: Opotřebení vložky | Zvětšení vrtání v důsledku opotřebení. | Zvětšení vrtání + silný profuk plynů (0,03 kg/s). |
| F4: Opotřebení pístních kroužků | Únik plynu. | Úprava hmotnostního průtoku profuku (0,02 kg/s). |
| F5: Zapečení kroužků | Zvýšené tření a selhání těsnění. | Změna průměru vrtání + zvýšení teploty vložky + profuk plynů. |
Analýza vysvětlitelnosti
Hlavní inovace této studie spočívá v přesunu pozornosti z "Co je to za poruchu?" na "Proč byla tato porucha diagnostikována?". Tuto schopnost jsme demonstrovali na analýze opotřebení pístních kroužků (F4):
- Lokální vysvětlení (Vodopádový graf): Vodopádový graf rozebírá konkrétní predikční logiku. Model například předpověděl "opotřebení kroužků", protože tepelný tok profuku (P06) a hmotnostní průtok profuku (P07) vykazovaly specifické hodnoty, čímž se zvýšila pravděpodobnost predikce této poruchy. To je v souladu s fyzikálními zákony: opotřebení kroužků ničí těsnost, což vede k úniku plynu (profuku).
- Globální vysvětlení (Včelí graf): Globální analýza odhaluje obecné zákonitosti, které se model naučil. Zjistili jsme, že nízká hodnota tlaku výfukových plynů před turbínou (P11) je silným indikátorem opotřebení kroužků. Z fyzikálního hlediska je to konzistentní: opotřebované kroužky vedou k úniku plynu z válce, čímž se snižuje energie dostupná pro pohon turbíny.
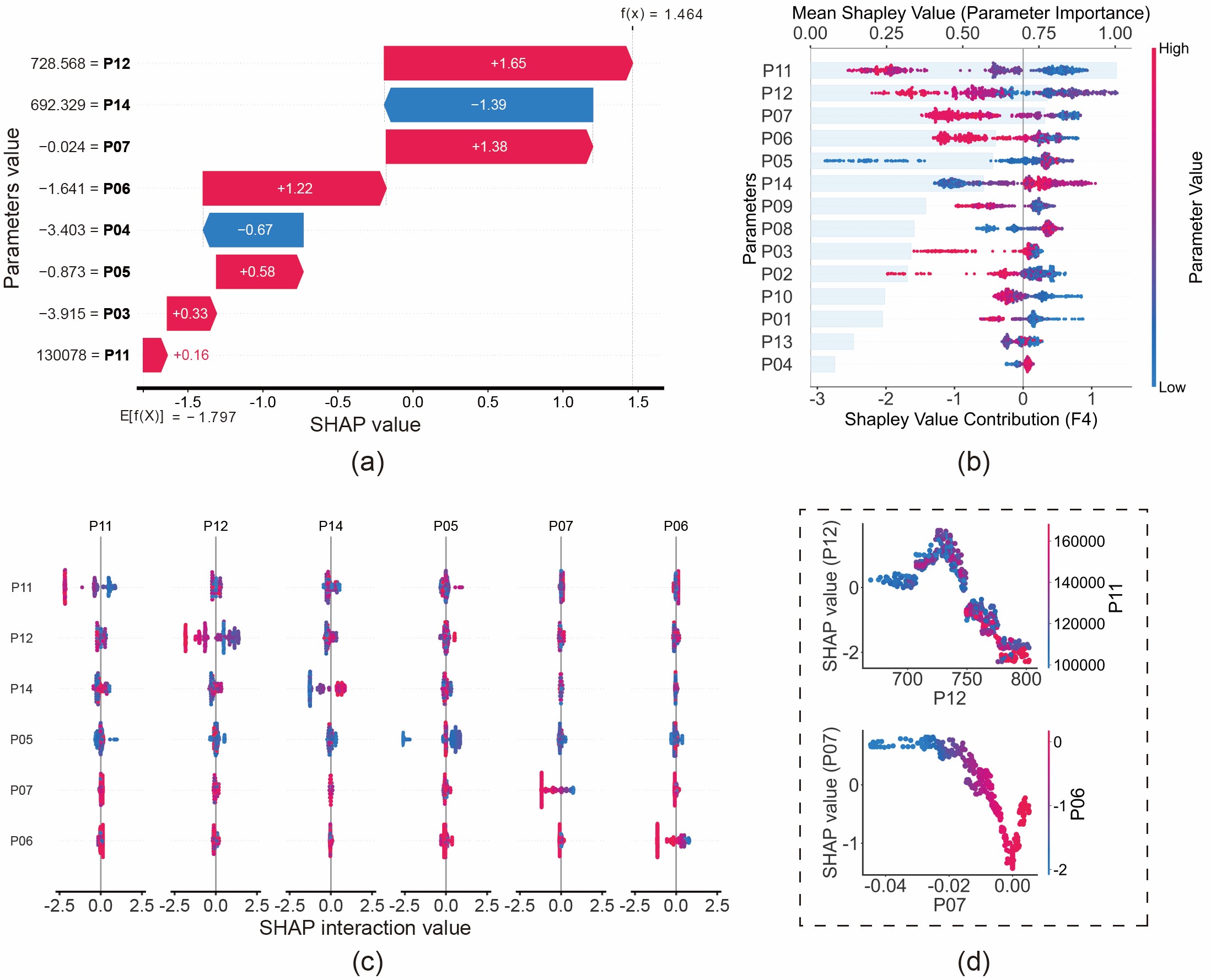
Obr. 11: Analýza poruchy opotřebení pístních kroužků (F4) na základě hodnot SHAP: (a) Vodopádový graf; (b) Včelí graf; (c) Interakční graf; (d) Graf závislosti.
Zobrazit kód vizualizace SHAP (Python)
Pokud vás zajímají detaily implementace výše uvedených grafů, zde je ukázkový kód pro generování vodopádového, včelího, interakčního a závislostního grafu.👇
Hlavní body výzkumu
Věříme, že tato práce přinesla následující klíčové příspěvky do tohoto oboru:
- Vytvoření parametrizovaných modelů pro pět typických poruch komponent spalovací komory lodních dieselových motorů.
- Ověření účinnosti metody SHAP porovnáním s několika metodami výběru příznaků.
- Poskytnutí nového pohledu na vysvětlitelnou diagnostiku poruch spojením metod založených na datech s termodynamickými mechanistickými modely.