دافع البحث
في مجال الهندسة البحرية وإدارة التنبؤ والصحة (PHM)، تواجه الصناعة عقبتين رئيسيتين طويلتي الأمد:
- ندرة البيانات: محركات الديزل البحرية (خاصة المحركات الرئيسية للسفن العابرة للمحيطات) هي قلب السفينة. يمكن أن يؤدي حدوث عطل خطير في البحر إلى فقدان قوة الدفع، أو الجنوح، أو حتى كوارث بحرية. لذلك، فإن عوامل الأمان في تصميمها عالية للغاية، واحتمالية حدوث أعطال خطيرة منخفضة جدًا بطبيعتها. بالإضافة إلى ذلك، تطبق الصناعة البحرية أنظمة صيانة وقائية صارمة (مثل الإصلاح الشامل المجدول بناءً على ساعات التشغيل). يتم استبدال الغالبية العظمى من الأجزاء القابلة للتآكل قسريًا قبل أن تفشل فعليًا وتولد بيانات أعطال. يؤدي هذا إلى وفرة في البيانات الصحية وبيانات التآكل المبكر، ولكن نقصًا حادًا في البيانات الحقيقية حول الفشل الكامل أو الأعطال الخطيرة.
- مشكلة "الصندوق الأسود": نظرًا لأن نماذج التعلم العميق تفتقر عادةً إلى الشفافية، يصعب على المهندسين الوثوق بها إذا لم يتمكنوا من تفسير الأسباب الفيزيائية للعطل. في صناعة الشحن التي تخضع لرقابة صارمة من قبل هيئات التصنيف، يعد هذا الغموض أمرًا حاسمًا. إذا أخطأ الذكاء الاصطناعي في تشخيص (أو فاته) تآكل المكبس أو كسر العمود المرفقي، ولم يتمكن النظام من تتبع ما إذا كان الخطأ نابعًا من تحيز البيانات أو عيب في الخوارزمية أو انحراف المستشعر، فإن عدم القدرة على التتبع هذا غير مقبول في تحقيقات الحوادث البحرية.
لمواجهة هذه التحديات، اقترحنا طريقة TSRF. من خلال دمج النماذج الميكانيكية القائمة على الفيزياء مع تقنيات القابلية للتفسير المتقدمة واستخدام نماذج محاكاة عالية الدقة لحل مشكلة ندرة البيانات، نضمن أن قرارات التشخيص تتوافق مع المبادئ الأساسية للديناميكا الحرارية.
المنهجية
يتضمن سير العمل في هذه الدراسة المراحل الأربع الرئيسية التالية (كما هو موضح في الشكل):
- النمذجة الديناميكية الحرارية: بدلاً من الاعتماد فقط على منصات الاختبار الفيزيائية، قمنا ببناء نموذج ديناميكي حراري أحادي البعد عالي الدقة لمحرك ديزل بحري سداسي الأسطوانات. تمت معايرة النموذج بدقة بناءً على بيانات التشغيل الحقيقية، مع الحفاظ على خطأ المحاكاة في حدود 5%.
- حقن الأعطال: بناءً على النموذج المعاير، قمنا بمحاكاة خمسة أعطال محددة لغرفة الاحتراق (مثل شقوق رأس الأسطوانة، تآكل المكبس، وما إلى ذلك) عن طريق ضبط المعلمات الفيزيائية، وبالتالي إنشاء مجموعة بيانات تغطي درجات مختلفة من أعطال المحرك الحقيقية.
- اختيار الميزات القائم على SHAP: استخدمنا قيم SHAP لتحديد الميزات الرئيسية كميًا، واخترنا 14 معلمة حاسمة تتحكم في قرار التشخيص.
- تشخيص التصنيف: باستخدام مجموعة البيانات المعززة فيزيائيًا هذه، قمنا بتدريب مصنف الغابة العشوائية (RF) وحققنا تشخيصًا عالي الدقة للأعطال.
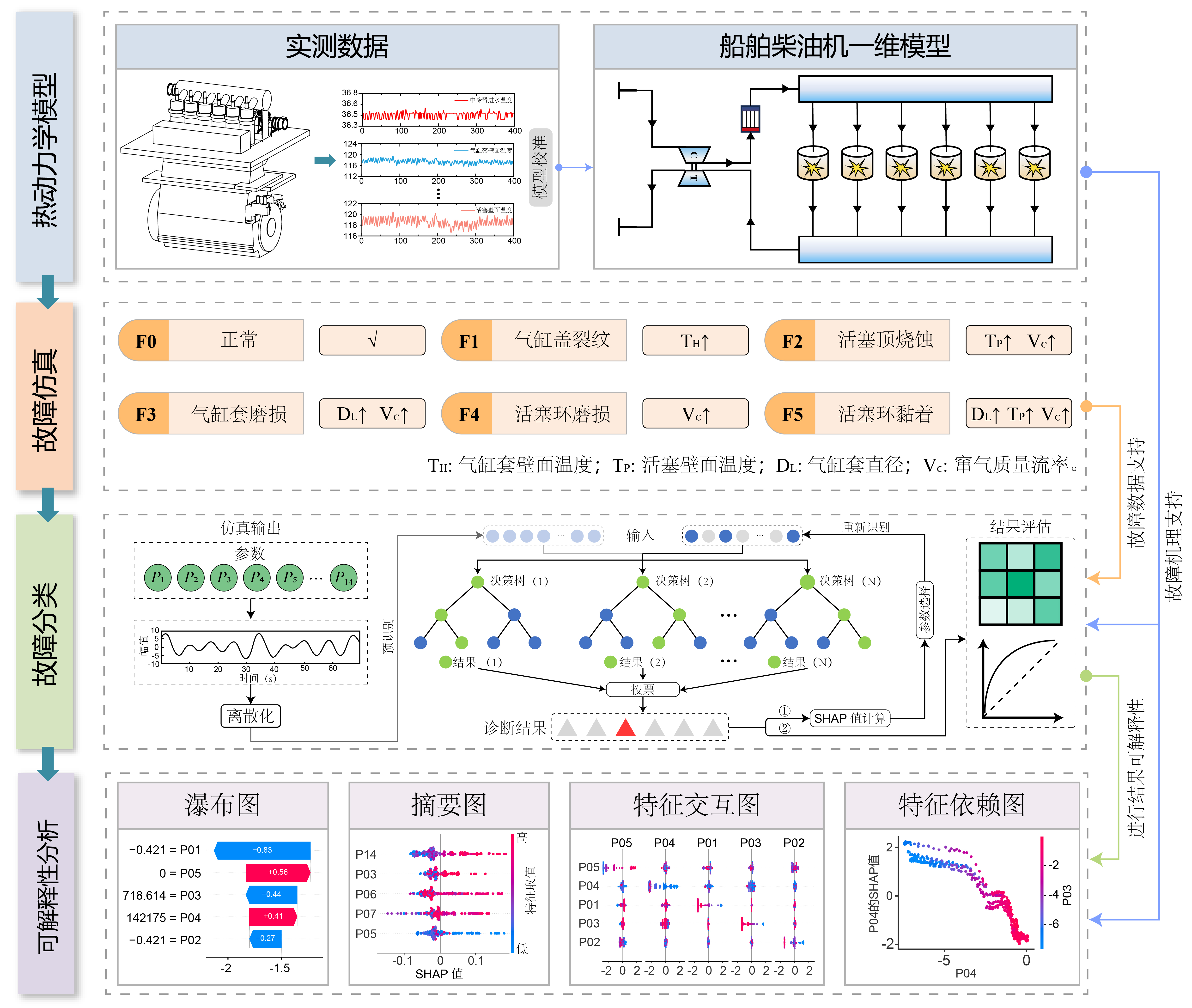
الشكل 1: هيكلية طريقة TSRF.
تفاصيل النمذجة الديناميكية الحرارية
لضمان دقة عالية، قمنا ببناء نموذج محاكاة لمحرك الديزل أحادي البعد. يوازن هذا النموذج الميكانيكي بين الدقة الفيزيائية وكفاءة الحساب المطلوبة لتوليد مجموعة البيانات.
طوبولوجيا النموذج
يتم تمثيل نظام المحرك كشبكة من خطوط الموائع والمكونات الوظيفية:
- وحدة الطاقة الأساسية: تكوين خطي، سداسي الأسطوانات، ثنائي الشوط.
- نظام الهواء: ترتبط متشعبات السحب/العادم (PL1, PL2) عبر شبكة أنابيب معقدة.
- نظام الشحن التوربيني: شاحن توربيني (TC1) مقترن بمبرد داخلي (CO1).
المعايرة والتحقق
قبل إجراء حقن الأعطال، تمت معايرة النموذج الأساسي بدقة بناءً على البيانات المقاسة.
- مصدر البيانات: بيانات تشغيل السفينة الحقيقية التي تم الحصول عليها من خلال وحدة الحصول على البيانات (DCM).
- التحقق: تم التحكم في انحرافات المعلمات الرئيسية (مثل الطاقة، درجة حرارة العادم) بدقة ضمن نطاق خطأ ±5% .
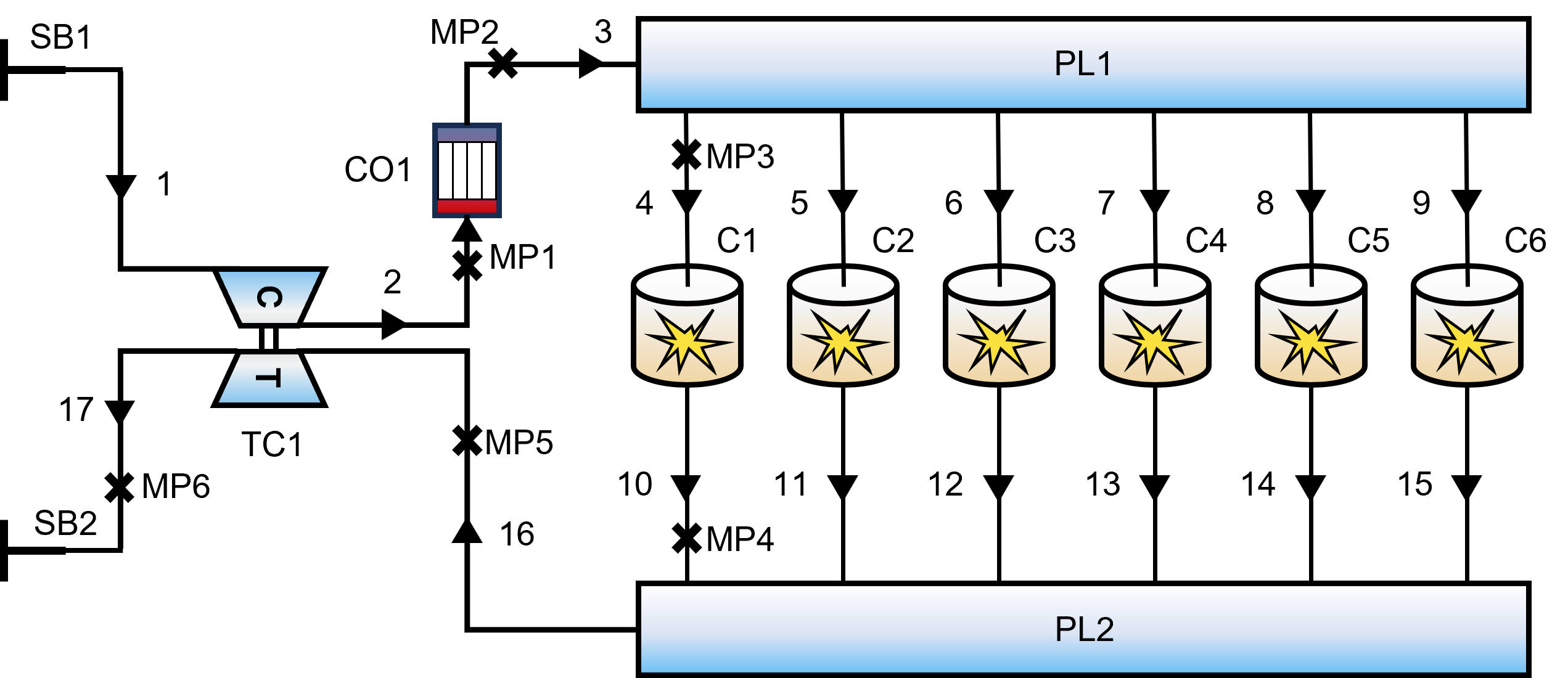
الشكل 2: مخطط للنموذج الديناميكي الحراري أحادي البعد لمحرك الديزل.
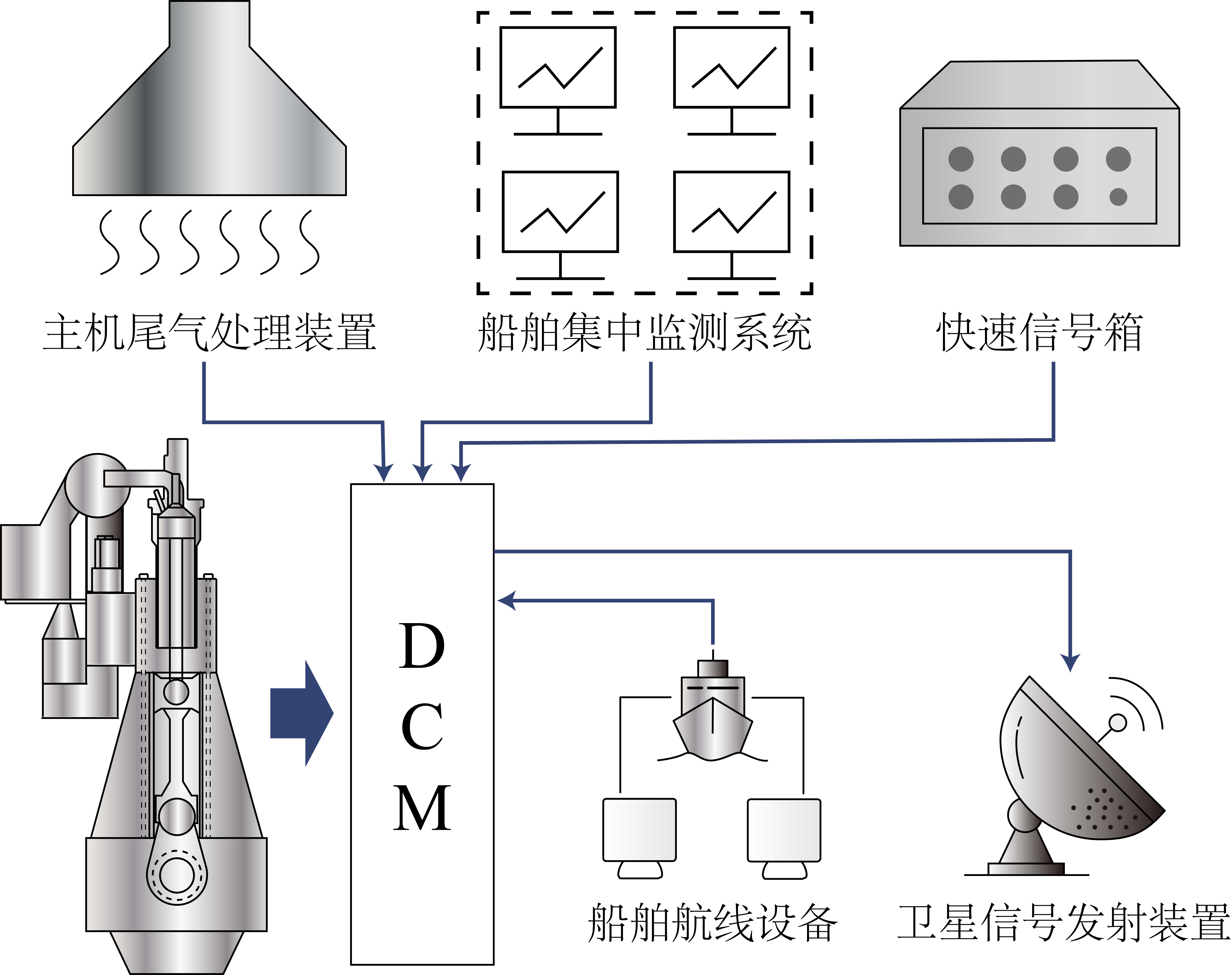
الشكل 5: وحدة الحصول على البيانات (DCM).
آلية حقن الأعطال
نظرًا لأن النماذج أحادية البعد لا يمكنها تمثيل العيوب الهيكلية ثلاثية الأبعاد بشكل مباشر، فقد اعتمدنا طريقة رسم الخرائط الظاهراتية لترجمة آليات التدهور الفيزيائي إلى انحرافات مكافئة في المعلمات الديناميكية الحرارية.
| نوع العطل | الآلية الفيزيائية | تنفيذ النمذجة |
|---|---|---|
| F1: شق في رأس الأسطوانة | إعاقة التوصيل الحراري. | رفع درجة حرارة سطح رأس الأسطوانة ($T_H$) إلى 346 درجة مئوية. |
| F2: تآكل المكبس (Ablation) | فقدان المواد وفشل الختم. | زيادة درجة حرارة المكبس ($T_P$) + تسرب غاز خفيف (Blow-by) (0.01 كجم/ثانية). |
| F3: تآكل البطانة | زيادة قطر التجويف بسبب التآكل. | زيادة التجويف + تسرب غاز شديد (0.03 كجم/ثانية). |
| F4: تآكل الحلقات | تسرب الغاز. | تعديل معدل تدفق كتلة تسرب الغاز (0.02 كجم/ثانية). |
| F5: التصاق الحلقات | زيادة الاحتكاك وفشل الختم. | تغيير قطر التجويف + زيادة درجة حرارة البطانة + تسرب الغاز. |
تحليل القابلية للتفسير
يكمن الابتكار الجوهري لهذه الدراسة في تحويل التركيز من "ما هو العطل؟" إلى "لماذا تم تشخيص هذا العطل؟". لقد أظهرنا هذه القدرة من خلال تحليل حالة تآكل حلقات المكبس (F4):
- التفسير المحلي (مخطط الشلال): يحلل مخطط الشلال منطق التنبؤ المحدد. على سبيل المثال، تنبأ النموذج بـ "تآكل الحلقات" لأن التدفق الحراري لتسرب الغاز (P06) ومعدل تدفق كتلة تسرب الغاز (P07) أظهرا قيمًا محددة، مما زاد من احتمالية التنبؤ بهذا العطل. هذا يتوافق مع القوانين الفيزيائية: تآكل الحلقات يدمر الختم، مما يؤدي إلى تسرب الغاز.
- التفسير العالمي (مخطط السرب): يكشف التحليل العالمي عن القوانين العامة التي تعلمها النموذج. وجدنا أن انخفاض ضغط العادم قبل التوربين (P11) هو مؤشر قوي على تآكل الحلقات. من الناحية الفيزيائية، هذا متسق: الحلقات المتآكلة تؤدي إلى تسرب الغاز من الأسطوانة، مما يقلل من الطاقة المتاحة لتشغيل التوربين.
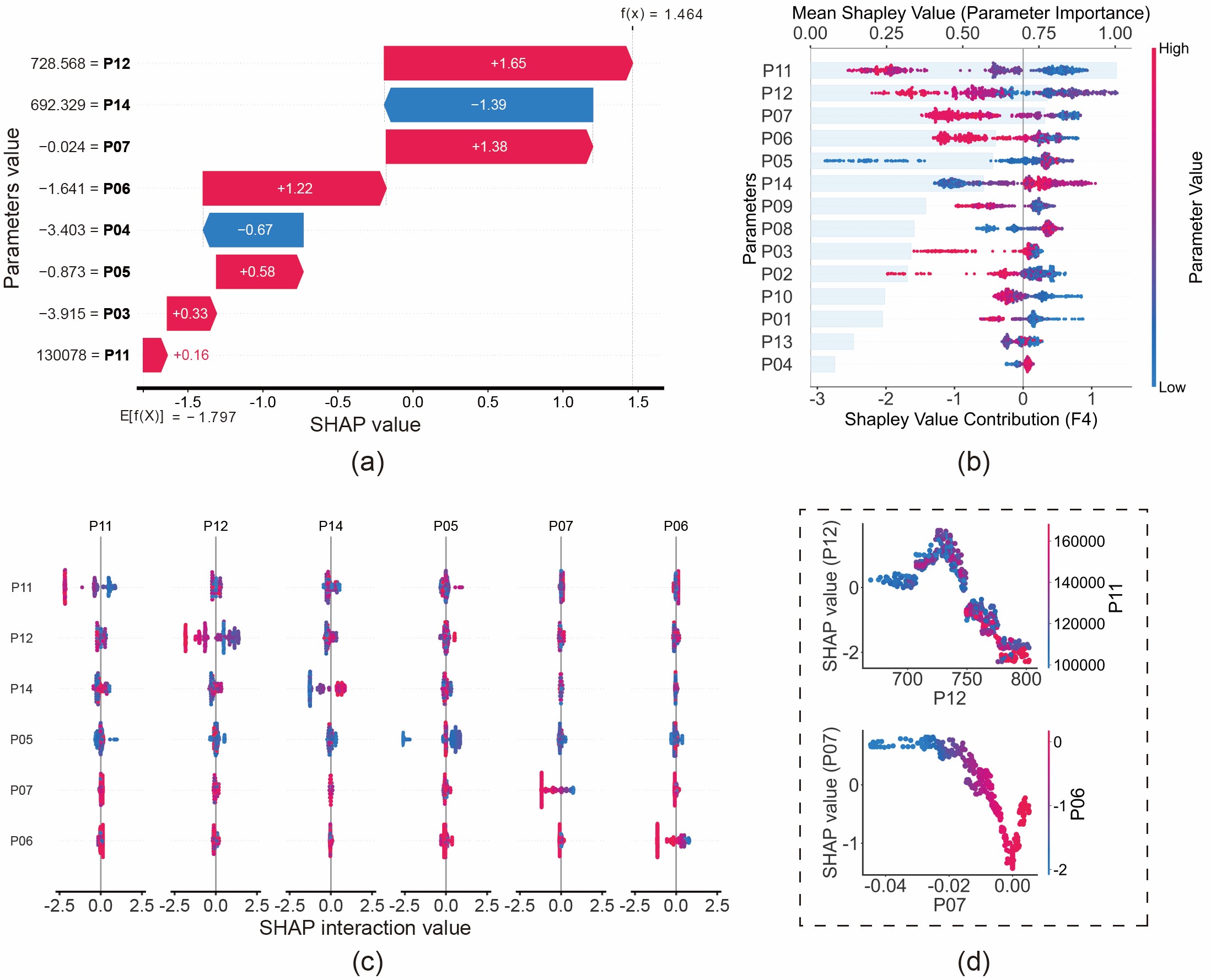
الشكل 11: تحليل عطل تآكل الحلقات (F4) بناءً على قيم SHAP: (أ) مخطط الشلال؛ (ب) مخطط السرب؛ (ج) مخطط التفاعل؛ (د) مخطط الاعتماد.
عرض كود تصور SHAP (بايثون)
إذا كنت مهتمًا بتفاصيل تنفيذ الرسوم البيانية أعلاه، فإليك مثال للكود لإنشاء مخططات الشلال والسرب والتفاعل والاعتماد.👇
أبرز النقاط البحثية
نعتقد أن هذا العمل قد قدم المساهمات الرئيسية التالية في هذا المجال:
- إنشاء نماذج ذات معاملات لخمسة أعطال نموذجية لمكونات غرفة الاحتراق في محركات الديزل البحرية.
- التحقق من فعالية طريقة SHAP من خلال المقارنة مع طرق اختيار الميزات المتعددة.
- توفير منظور جديد لتشخيص الأعطال القابل للتفسير من خلال دمج الأساليب القائمة على البيانات مع النماذج الميكانيكية الديناميكية الحرارية.