Motivation
In the fields of marine engineering and Prognostics and Health Management (PHM), the industry faces two persistent bottlenecks:
- Data Scarcity: Marine diesel engines, especially the main engines on ocean-going vessels, are the heart of a ship. Any serious malfunction at sea risks a loss of propulsion, grounding, or even a major maritime disaster. For this reason, they are designed with extremely high safety margins, making the likelihood of a serious breakdown naturally low. In addition, the shipping industry follows strict preventive maintenance schedules, such as inspections based on running hours. Most parts prone to wear are replaced long before they actually fail or generate fault data. As a result, while we possess a vast amount of data on healthy engines and early wear patterns, there is a distinct lack of real-world data on total system failures.
- The "Black Box" Problem: Since deep learning models typically lack transparency, engineers find it difficult to trust them without an explanation of the physical causality behind a fault. This opacity is particularly critical in the shipping industry, which is subject to rigorous oversight by classification societies. If an AI misdiagnosis precipitates a catastrophic failure like cylinder scuffing or a crankshaft fracture, and the system cannot identify whether the error stemmed from data bias, algorithmic flaws, or sensor drift, such untraceability is unacceptable in maritime accident investigations.
To address these challenges, we propose the TSRF method. This approach integrates physics-based mechanistic models with advanced explainability techniques. By leveraging high-fidelity simulation models to generate synthetic data, we effectively resolve the issue of data scarcity and ensure that diagnostic decisions adhere to fundamental thermodynamic principles.
Methodology
Our workflow consists of four distinct stages, as illustrated below:
- Thermodynamic Modeling: Rather than relying solely on physical test rigs, we constructed a high-fidelity 1-D thermodynamic model of a 6-cylinder marine diesel engine. The model was rigorously calibrated using real-world operational data, keeping simulation errors within 5%.
- Fault Injection: Based on the calibrated model, we adjusted the physical parameters to simulate five distinct combustion chamber faults, such as cylinder head cracks and piston ablation. We then generated a dataset that captures the full spectrum of fault severities observed in actual engines.
- Feature Selection via SHAP: We utilized SHAP values to quantitatively identify the critical features, including the 14 key parameters that drive the diagnostic decision.
- Classification: A Random Forest (RF) classifier was trained using this physics-enhanced dataset to achieve high diagnostic precision.
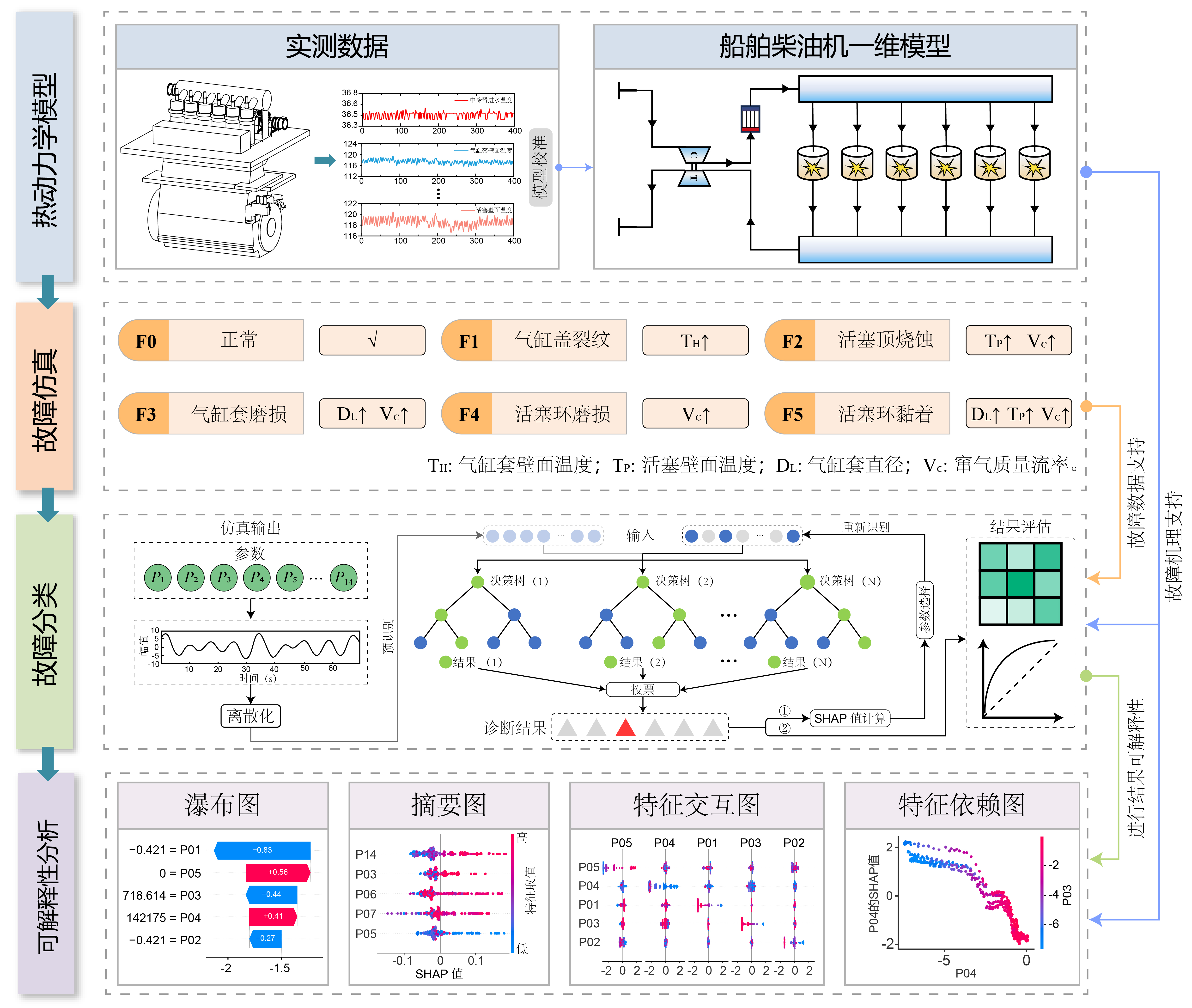
Figure 1: The structure of the proposed TSRF method.
Thermodynamic Modeling Details
To ensure high fidelity, we constructed a one-dimensional simulation model. This mechanism model balances physical accuracy with the computational efficiency required for dataset generation.
Model Topology
The engine is discretized into a network of flow pipes and functional components:
- Core Power Unit: 6-cylinder, 2-stroke inline configuration.
- Air Path System: Intake/Exhaust manifolds (PL1, PL2) connected via complex piping networks.
- Boosting System: Turbocharger (TC1) coupled with an intercooler (CO1).
Calibration & Validation
Before fault injection, the baseline model was rigorously calibrated against empirical data.
- Data Source: Real-world vessel data acquired via Data Collecting Module (DCM).
- Validation: The deviation for critical parameters (e.g., Power, Exhaust Temp) was maintained within a ±5% error margin.
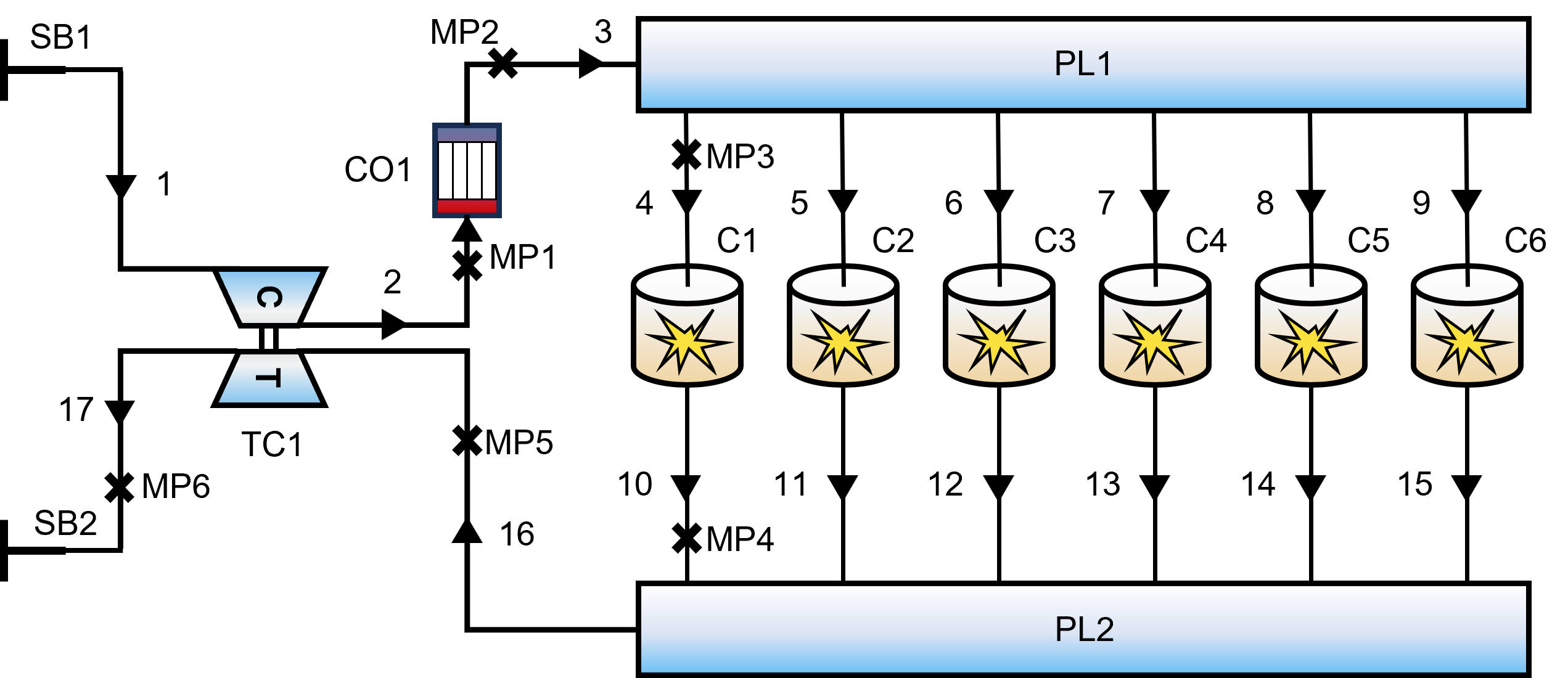
Figure 2: One-dimensional thermodynamic model of the diesel engine.
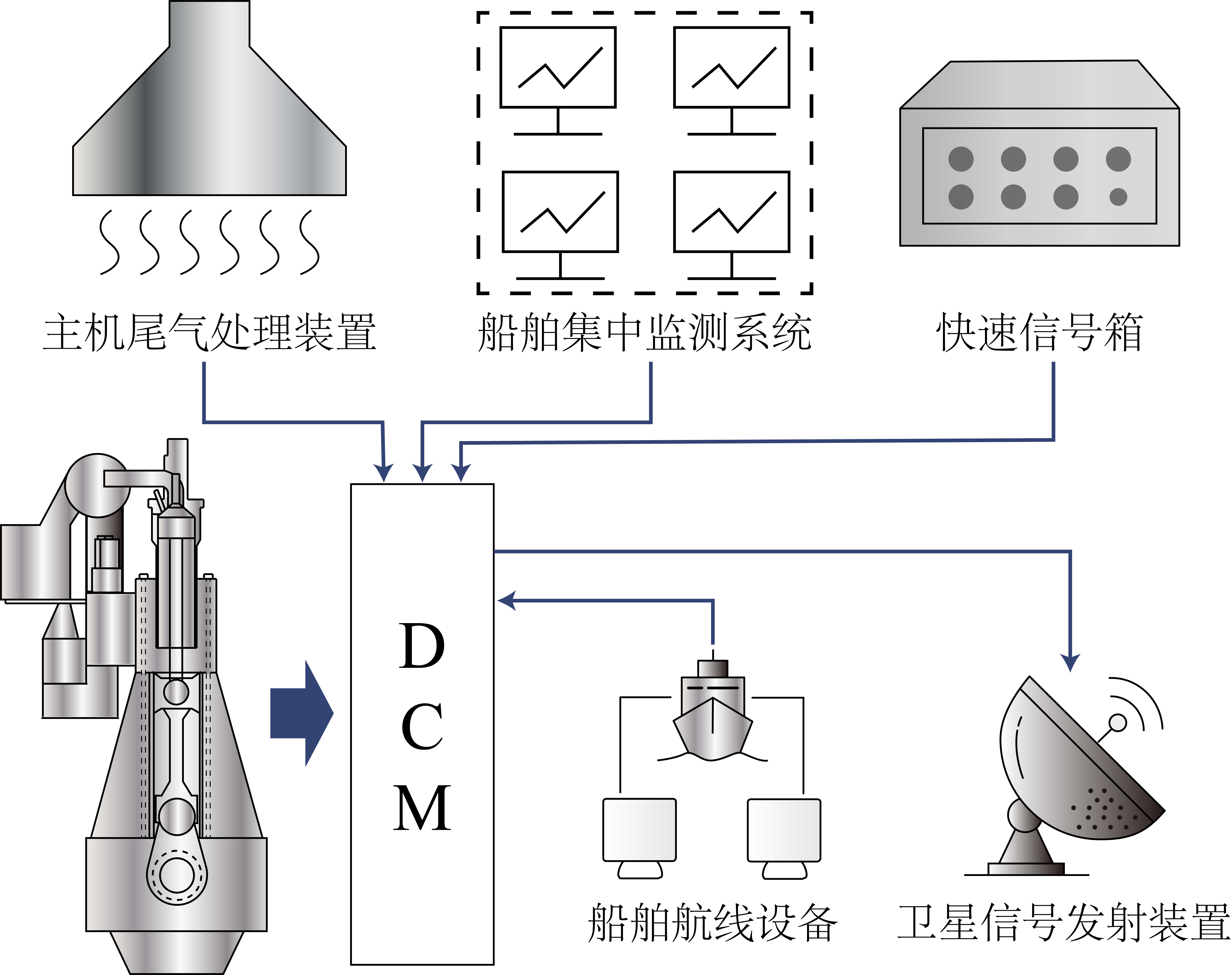
Figure 5: Data Collecting Module (DCM).
Fault Injection Mechanism
Since 1-D models cannot directly represent 3D structural defects, we employed a phenomenological mapping approach, translating physical degradation mechanisms into equivalent thermodynamic parameter shifts.
| Fault Type | Physical Mechanism | Modeling Implementation |
|---|---|---|
| F1: Head Cracking | Disrupted thermal conduction. | Elevating Cylinder Head Surface Temp ($T_H$) to 346°C. |
| F2: Piston Ablation | Material loss & seal compromise. | Increasing Piston Temp ($T_P$) + minor blow-by (0.01 kg/s). |
| F3: Liner Wear | Abrasive wear increases bore. | Increasing Bore Diameter + substantial blow-by (0.03 kg/s). |
| F4: Ring Wear | Gas leakage only. | Modulation of Blow-by Mass Flow Rate (0.02 kg/s). |
| F5: Ring Sticking | Friction & seal failure. | Bore Dia. change + Elevated Liner Temp + Blow-by. |
Explainability Analysis
A key innovation of our work is shifting the focus from "What is the fault?" to "Why is this the fault?". We demonstrate this capability through a case study on Piston Ring Wear (F4):
- Local Interpretation (Waterfall Plot): The waterfall plot explains specific predictions. For instance, the model predicts "Ring Wear" because Blow-by Heat Flow (P06) and Blow-by Mass Flow (P07) exhibit specific values that increase the probability. This aligns with physics: ring wear compromises the seal, leading to gas leakage (blow-by).
- Global Interpretation (Beeswarm Plot): Global analysis reveals the general rules learned by the model. We found that low values of Pre-turbo Exhaust Pressure (P11) are strong indicators of Ring Wear. Physically, this is consistent: worn rings allow gas to leak from the cylinder, reducing the energy available to the turbine.
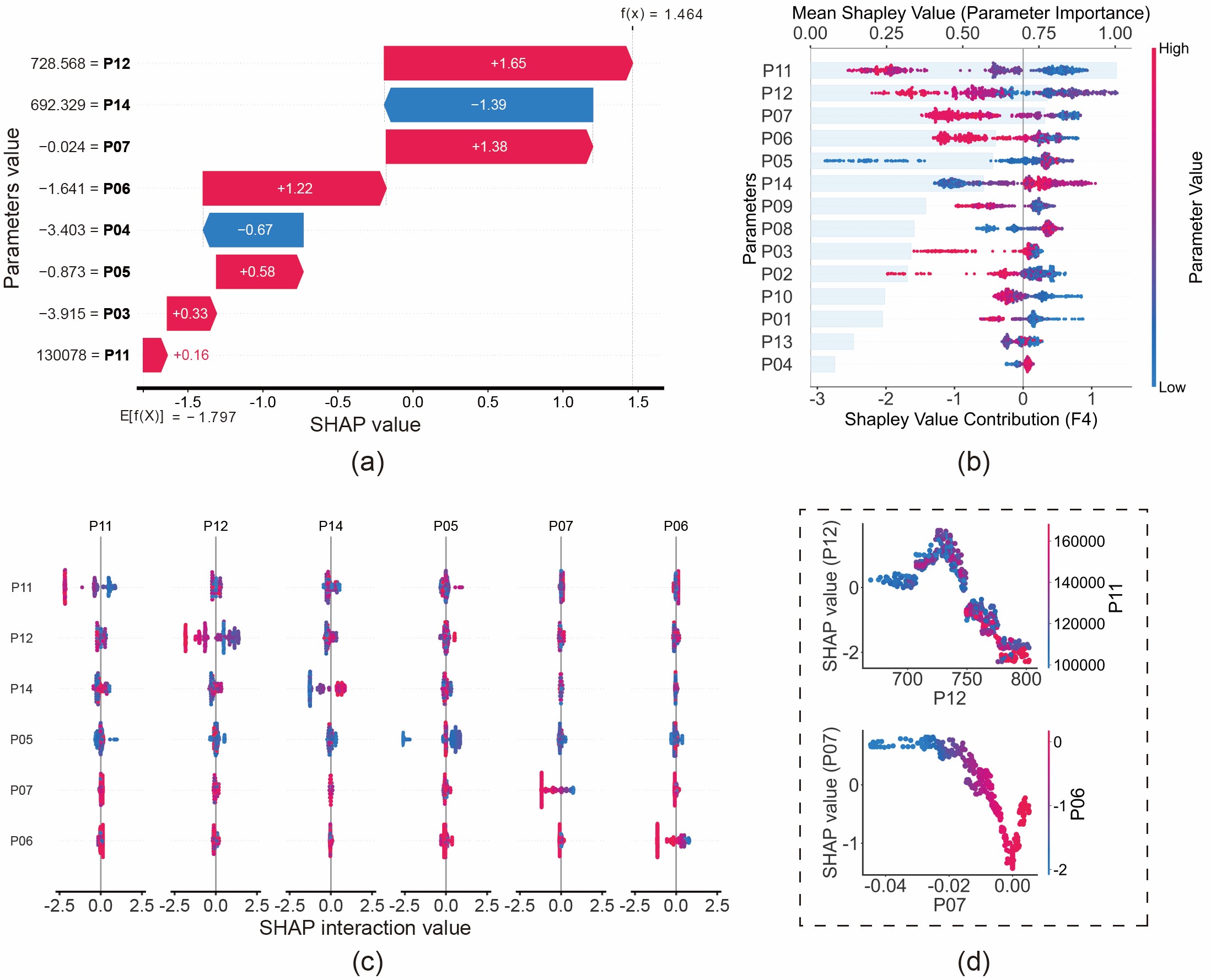
Figure 11: Fault analysis of piston ring wear (F4) based on SHAP values: (a) Waterfall plot; (b) Beeswarm plot; (c) Interaction plot; (d) Dependence plot.
Click to view SHAP Visualization Code (Python)
If you are interested in the implementation details of the figures above, here is the sample code used to generate the Waterfall, Beeswarm, Interaction, and Dependence plots.👇
Research Highlights
We believe this work offers several key contributions to the field:
- Performs parameterized modeling of five faults in marine diesel engine combustion chamber.
- Evaluated the effectiveness of SHAP method through comparison with multiple feature selection methods.
- A novel insight into interpretable fault diagnosis is provided by integrating data-driven method with thermodynamic model.